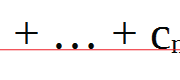Калькулятор соотношений

Калькулятор Процентов

Что если % из ?		Результат:
это какой процент от ?		Ответ: %
это % от чего?		Ответ:

Как процентные соотношения помогают в реальной жизни

Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:

1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.

Решение:

Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:

(800 — 650) ÷ 650 ⋅ 100 = 23,08%

Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.

Теперь давайте применим тоже самое ко второму месяцу:

(1200 — 800) ÷ 800 ⋅ 100 = 50%

Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50). Теперь понятно,что доходы Тома растут.

2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.

Решение:

В табличке сказано, что

$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$

$Продано\ длина = \frac{60 \times 30}{100} = 18м$

Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.

Примеры:

1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?

Решение:

Общее количество карточек = 32 + 25 + 47 = 104

Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%

Процентное соотношение футбольных карточек = 25/104 x 100 = 24%

Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%

Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек. 2

На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

Решение:

Общее количество = 3×3 + 2×4 = 17 баллов

Полученные балы = 2×3 + 4 = 10 баллов

Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%

3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?

Решение:

Увеличение цены равно 40 x 20/100 = \$8

Новая цена равна 40 + 8 = \$48

Процентное соотношение (или отношение) двух чисел — это отношение одного числа к другому умноженное на 100%.

Процентное отношение двух чисел можно записать следующей формулой:

Как в Excel посчитать разницу в процентах между двумя числами?

Разница двух чисел в процентах в Экселе (Excel).

Как в Экселе (Excel) узнать на сколько одно число больше или меньше другого?

Часто узнать насколько процентов одно число больше другого требуется при оценке значений различных величин и при этом иногда знак процентов не допустим, в этом случае формат ячейки должен быть текстовым.

Чтобы определить насколько процентов одно число больше другого в текстовом формате надо воспользоваться функцией ТЕКСТ с указанием формата «0.00%» или «0%» с последующей заменой знака % на слово

Если значения записаны в колонках таблицы A и B

то формула будет такая:

=ТЕКСТ((A2-B2)/B2;»0.00%»)

с заменой знака % на слово получится формула:

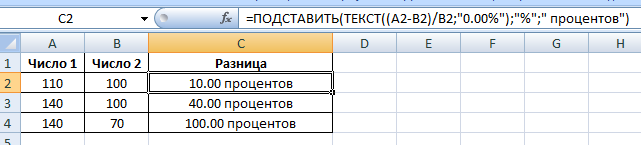
При работе с данными в Excel иногда возникает необходимость посчитать разницу в процентах между двумя числами.

Например, нам нужно узнать, на сколько процентов (за определённый период) увеличилась или уменьшилась цена товара, прибыль предприятия и т.д.

Рассмотрим, как это можно сделать.

Разница двух чисел в процентах в Excel

Посчитаем в программе Excel в качестве примера динамику дохода 1 и 2 цеха предприятия — узнаем, на сколько процентов увеличился или уменьшился доход каждого цеха в 2016 году по сравнению с 2015.

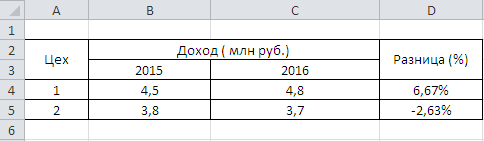
Для нахождения разницы между числами в процентах в Экселе нужно сделать следующее:

1) Установить формат ячейки с результатом (в нашем случае D4 и D5) как процентный.

Для этого щёлкаем правой кнопкой мыши на ячейке и выбираем «Формат ячеек».

На вкладке «Число» выбираем «Процентный».

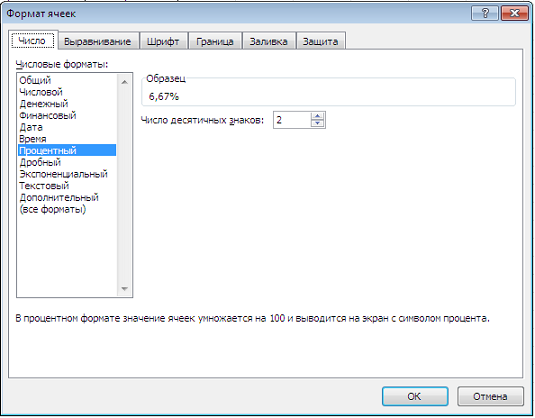
Также процентный формат можно сделать на панели инструментов Excel.

2) Вообще, посчитать разницу двух чисел в процентах можно с помощью двух формул:

Разница = (Число 2 — Число 1) / Число 1 * 100%.

Разница = ((Число 2 / Число 1) — 1) * 100%.

В нашем случае «Число 1» — это старое значение (доход 2015 года), «Число 2» — это новое значение (доход 2016 года).

В ячейку D4 пишем формулу: (D4-C4) / C4.

В ячейку D5 пишем формулу: (D5-C5) / C5.

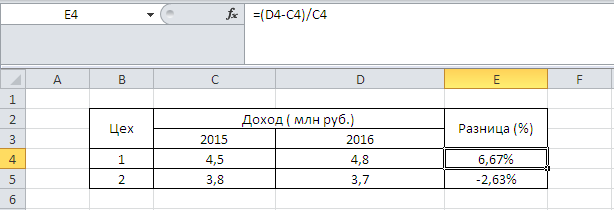
Мы видим, что прибыль 1 цеха увеличилась на 6,67%, прибыль 2 цеха уменьшилась на 2,63%.

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Калькулятор Процентов

Что если % из ?		Результат:
это какой процент от ?		Ответ: %
это % от чего?		Ответ:

Как процентные соотношения помогают в реальной жизни

Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:

1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.

Решение:

Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:

(800 — 650) ÷ 650 ⋅ 100 = 23,08%

Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.

Теперь давайте применим тоже самое ко второму месяцу:

(1200 — 800) ÷ 800 ⋅ 100 = 50%

Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50). Теперь понятно,что доходы Тома растут.

2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:

Пример:

Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.

Решение:

В табличке сказано, что

$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$

$Продано\ длина = \frac{60 \times 30}{100} = 18м$

Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.

Примеры:

1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?

Решение:

Общее количество карточек = 32 + 25 + 47 = 104

Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%

Процентное соотношение футбольных карточек = 25/104 x 100 = 24%

Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%

Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек. 2

На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?

Решение:

Общее количество = 3×3 + 2×4 = 17 баллов

Полученные балы = 2×3 + 4 = 10 баллов

Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%

3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?

Решение:

Увеличение цены равно 40 x 20/100 = \$8

Новая цена равна 40 + 8 = \$48

Увеличение/Уменьшение процентного соотношения

Когда число увеличивается относительно другого числа, то величина увеличения представляется как:

Увеличение = Новое число — Старое число

Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:

Уменьшение = Старое число — Новое число

Увеличение или уменьшение числа всегда выражается на основании старого числа.Поэтому:

%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число

%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число

Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно

$\frac{120 — 80}{80} \times 100 = 50\%$

Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:

$\frac{120 — 100}{120} \times 100 = 16,67\%$

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь    означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Как в Эксель посчитать процент от числа

Простой расчет – получаем процент от одного числа. В ячейку A1 введем число, например 70. В ячейку B1 введем второе число, например 38. Вопрос, какой процент составляет число 38 от числа 70? Установим процентный формат для ячейки C1, в этой же ячейке нужно прописать формулу:

Формула вводится после знака = и отображается в строке формул. В ячейке A3 отобразится результат.

Усложняем задачу. Нужно рассчитать 5% от некоторых чисел. Пусть это будет 5 чисел в таблице. Введем в ячейку C1 значение 5%. В ячейку B1 введем формулу:

И выполним автозаполнение. Таким образом, в столбце B у нас будут значения соответствующие 5 процентам от числа в столбце A.

Знаки $ фиксируют ячейку C1. То есть, изменив значение с 5% до 8% (или иное) значения в столбце B пересчитаются автоматически.

Другой пример расчета процентов Excel

Итак, нам необходимо определить, какой процент составляют реализованные товары от общего количества продуктов на складе.

Для этого требуется выполнить следующие действия:

• В ячейку D2 вписать формулу =С2/D2 (количество проданных товаров/общее число продуктов) и нажать клавишу Enter.
• Чтобы не тратить время, рекомендуется воспользоваться функцией автозаполнения– растянуть формулу вниз настолько, насколько необходимо.
• Выделить все заполненные ячейки в столбце D и установить процентный формат.
• Оценить результат:

Выбрать процентный формат для ячейки можно четырьмя способами:

Выделив необходимые ячейки, перейти в контекстное меню правой клавишей мыши

Обратите внимание, что в этом случае есть возможность самостоятельно настроить количество знаков после точки.
Воспользоваться комбинацией клавиш Ctrl+Shift+5.
Выбрать формат во вкладке «главная» на панели задач.
Вписать число со знаком % — программа самостоятельно подберет нужный формат.. Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении

Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число

Иногда возникает обратная ситуация – необходимо определить, сколько составляет процент проданных товаров в числовом значении. Для этого достаточно выделить ячейку, для которой требуется получить результат, и умножить процент на целое число.

Определение процентного соотношения чисел

Вычислить процентное соотношение чисел в Excel очень просто! Необходимость выполнения этой задачи возникает достаточно часто – например, в случае, когда нужно оценить изменение уровня продаж за прошлый и текущий период.

Чтобы понять, насколько увеличились продажи в сентябре, необходимо сделать следующее:

• Задать в ячейке D2 формулу =(С2-B2)/B2 и нажать клавишу Enter.
• Протянуть D2 вниз на нужное количество строк.
• Выделить полученные данные и перевести в процентный формат любым удобным способом.

Положительное значение в столбце D показывает прибыль, отрицательное – соответственно, убыток.

Чтобы наглядно оценить результаты деятельности, можно сделать диаграмму. Для этого надо выделить столбец с процентами и выбрать тип диаграммы во вкладке «вставка».

Разница процентов в Экселе, как вычесть процент

Приведу другой пример, аналогичный предыдущему. Иногда нам нужно рассчитать разницу в процентах. Например, в 2017 году мы продали товаров на 2902345 рублей, а в 2018 году на 2589632 рублей.

Сделаем заготовку. И произведем расчеты.

В ячейке C2 введем формулу:

Данная форма показывает разницу между суммами в процентах. В данном примере мы продали товар в 2018 году на сумму меньшую, чем в 2017 году на 10,77%. О меньшей сумме свидетельствует знак минус. Если знак минус отсутствует, значит мы продали на большую сумму.

Если у вас много данных советую закрепить область в Excel.

Как посчитать процент выполнения плана в Excel

Процент выполнения плана в целом считается так же, как я описывал выше. Но давайте разберемся на более конкретном примере. А именно на плане учета рабочего времени.

Пример будет простой. Сотрудник получает заработную плату 10000 рублей в месяц в зависимости от процента отработанных дней в месяце. А так же сотрудник получает премию в размере 8000 в зависимости от выполнения плана продаж.

Сделаем таблицу для расчетов.

Далее все довольно просто. Что бы рассчитать процент выполнение нужно факт разделить на план.

Соответствующий процент умножить на ставку, а затем суммировать. Конечна сумма будет оплатой труда сотрудника за месяц.

Процентное соотношение двух чисел

Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:

m / n × 100 = p,

где m – размер части, n – размер целого, p – процент.

Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.

Примеры расчета процентов

Допустим, у нас есть 200 кг сахара. Мы хотим узнать:

• сколько сахара необходимо отгрузить, если требуется поставить 37 % от исходной массы;
• 3 кг сахара просыпалось, и требуется указать процент потерянного товара.

Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.

Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2 %.

Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18 % от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

1000 – 100%; 500 – x%. Получаем: X=(500*100)/1000. X=50 %.

Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Область применения программы

Выделить часть от любой величины – одна из самых распространенных задач во всех сферах жизни. Действие выполнялось на интуитивном уровне с момента совершения первого обмена в рамках одной семьи. На государственном уровне доля от целого была внедрена древнеримским императором Октавианом Августом. Он принял закон о налогообложении в виде сотой части от прибыли. Впоследствии долевой эквивалент стал неотъемлемой частью всех точных наук.

Безразмерная величина нашла наиболее широкое применение в экономике и статистике. Коммерческие сделки, переводы, налоги, комиссионные вознаграждения, анализ всевозможных количественных изменений в социуме невозможны без выделения долей из различных показателей. В повседневной жизни, человек ежедневно сталкивается с процентами. Самый простой пример – вечерние скидки в крупных магазинах или сезонные в бутиках анонсируются в виде части от первоначальной стоимости. Клиенту предлагается самостоятельно перевести % в реальные цифры. Теперь это можно сделать за секунды с помощью сервиса.

Процентное соотношение двух чисел

Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:

m / n × 100 = p,

где m – размер части, n – размер целого, p – процент.

Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.

Примеры расчета процентов

Допустим, у нас есть 200 кг сахара. Мы хотим узнать:

• сколько сахара необходимо отгрузить, если требуется поставить 37 % от исходной массы;
• 3 кг сахара просыпалось, и требуется указать процент потерянного товара.

Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.

Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2 %.

Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18 % от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.

Заключение

Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе

Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.

Например, вычислить, сколько процентов составляет число 52 от числа 400.

По правилу: 52: 400 * 100 — 13 (%).

Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).

Решения задач на процентное отношение двух чисел редко предполагают только одно действие. Чаше решение таких задач состоит из 2-3 действий.

1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?

1 200 изделий — это план завода, или 100% плана.

1) Сколько изделий изготовил завод сверх плана?

2 300 — 1 200 = 1 100 (изд.)

2) Сколько процентов от плана составят сверхплановые изделия?

1 100 от 1 200 => 1 100: 1 200 * 100 = 91,7 (%).

1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?

2 300 от 1 200 => 2 300: 1 200 * 100 = 191,7 (%).

2) На сколько процентов перевыполнен план?

2. Урожайность пшеницы в хозяйстве за предыдущий год составила 42 ц/га и была занесена в план следующего года. В следующем году урожайность снизилась до 39 ц/га. На сколько процентов был выполнен план следующего года?

42 ц/га — это план хозяйства на этот год, или 100% плана.

1) На сколько снизилась урожайность по сравнению

2) На сколько, процентов план не довыполнен?

3 от 42 => 3: 42 * 100 = 7.1 (%).

3) Насколько процентов выполнен план этого года?

1) Сколько процентов составляет урожайность этого гола по сравнению с планом?

Задача была сформулирована следующим образом

«Соотношения между двумя числами А и В:

1. Сколько процентов составляет А от В и наоборот;
2. Сколько процентов составляет разница между А и В относительно А и относительно В;
3. Еще какие-то соотношения между А и В»

Собственно, придумалось несколько соотношений, которые и считает этот простой калькулятор. Там, где значения в долях единицы (как результат деления чего-то на чего-то), умножаем на 100 и получаем проценты.

Анонимный Число А на 56% меньше числа В, которое в 2,2 раза меньше числа С. Какой процент числа С относительно числа А?
NMitra A = B — 0,56 ⋅ B = B ⋅ (1 — 0,56) = 0,44 ⋅ B
B = A: 0,44
С = 2,2 ⋅ B = 2,2 ⋅ A: 0,44 = 5 ⋅ A
C в 5 раз больше A
C на 400% больше A
Анонимный Помогите. В 2001 выручка возросла по сравнению с 2000 на 2 процента, хотя планировали в 2 раза. На сколько процентов недовыполнен план?
NMitra А — 2000 год
Б — 2001 год
Б = A + 0,02A = A ⋅ (1 + 0,02) = 1,02 ⋅ A
Б = 2 ⋅ А (план)
2 — 100%
1,02 — х%
х = 1,02 ⋅ 100: 2 = 51% (выполнен план)
100 — 51 = 49% (недовыполнен план)
Анонимный Помогите ответить на вопрос. Арбуз содержит 99% влажность, но после усушки (положить на солнышко на несколько дней) влажность его составляет 98%. На сколько % изменится ВЕС арбуза после усушки?
Если рассчитывать математическим путем, то получается, что у меня арбуз совсем усох.
Например: при весе в 20 кг вода составляет 99% массы, то есть сухой вес равен 1% = 0,2 кг.
Тут арбуз теряет жидкость, и состоит уже на 98%, следовательно, сухой вес равен 2%. Но сухой вес не может измениться из-за потери воды, поэтому он как и прежде равен 0,2 кг. 2%=0,2 => 100%=10 кг.
Анонимный Подскажите, пожалуйста, как вычислить сам процент в диапазоне 2-ух значений? Скажем, какой процент у числа 37 в диапазоне значений 22-63? Мне нужна формула для приложения, раньше решал такие задачи за пару минут, а сейчас мозг усох). Выручайте.
NMitra У меня так выходит:
процент = (число — z0) ⋅ 100: (z1-z0)
z0 — начальное значение диапазона
z1 — конечное значение диапазона
Например,
х = (37-22) ⋅ 100: (63-22) = 1500: 41 = 37%
Для примера ниже сходится

10	20	30	40	50	60	70	80	90	100
2	3	4	5	6	7	8	9	10	11	12

35	50%	10	45
16	23%	4,6	20,6
18	26%	5,2	23,2
1	1%	0,2	1,2
70	100%	20	90

35	50%	10	45	67,5
16	23%	4,6	20,6	30,9
18	26%	5,2	23,2	34,8
1	1%	0,2	1,2	1,8
70	100%	20	90	135