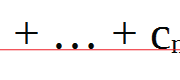Округлить до 2 знаков после запятой (только при необходимости)

Содержание:

Решение без знаков после запятой: javascript количество знаков после запятой
Методы
Сравнение чисел
- Основные математические операции
Сравнение чисел
- Основные математические операции
Description
Как проверить является ли переменная числом
Способы записи числа
- Шестнадцатеричные, двоичные и восьмеричные числа
Как явно преобразовать строку в число?
Примеры
- Пример: использование метода Math.ceil()
- Пример: корректировка округления десятичных дробей
Rounding the Number
- Rounding to the Nearest Integer
- Rounding to Arbitrary Levels of Precision
Round() в Go 1.10
Неточные вычисления
Привязка к диапазону
8 ответов:
Округление в большую сторону до ближайшего целого числа
- Округление до ближайшего кратного числа

Решение без знаков после запятой: javascript количество знаков после запятой

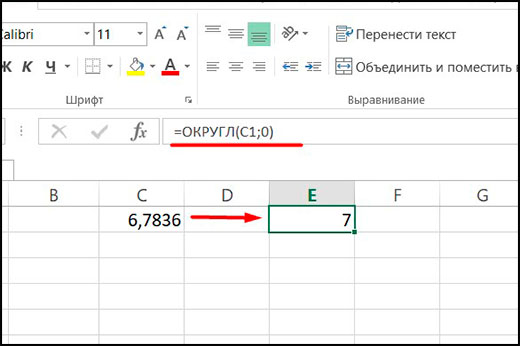
Если же знаки после запятой нужно полностью откинуть, то есть нужно округлить дробное число до целого, то можно использовать функции класса Math: round, ceil и floor.
Round — округляет в большую или меньшую сторону (в зависимости от числа). Если значение после запятой больше половины, то округлит в большую сторону, если меньше — в меньшую. То есть если 0.51 — станет 1, если 0.49 — 0.

Ceil — от англ. потолок округляет всегда в большую сторону.

Floor — от англ. пол округляет всегда в меньшую сторону.

Var num = 1538.9891200153;
num_str=Math.round(num); //num_str=1539;
num_str=Math.floor(num); //num_str=1538;
num_str=Math.ceil(num); //num_str=1539;

Часто вычисления дают результаты, которые не соответствуют пределам нужных диапазонов. В результате нужно осуществлять JavaScript округление
до определенного значения.

Методы

Как округлить результат в excel

Обратите внимание, что тригонометрические функции (, , , , , и ) принимают в параметрах или возвращают углы в радианах. Для преобразования радианов в градусы, поделите их на величину ; для преобразования в обратном направлении, умножьте градусы на эту же величину

Обратите внимание, что точность большинства математических функций зависит от реализации. Это означает, что различные браузеры могут дать разные результаты, более того, даже один и тот же движок JavaScript на различных операционных системах или архитектурах может выдать разные результаты

Возвращает абсолютное значение числа.

Возвращает арккосинус числа.

Возвращает гиперболический арккосинус числа.

Возвращает арксинус числа.

Возвращает гиперболический арксинус числа.

Возвращает арктангенс числа.

Возвращает гиперболический арктангенс числа.

Возвращает арктангенс от частного своих аргументов.

Возвращает кубический корень числа.

Возвращает значение числа, округлённое к большему целому.

Возвращает количество ведущих нулей 32-битного целого числа.

Возвращает косинус числа.

Возвращает гиперболический косинус числа.

Возвращает Ex, где x — аргумент, а E — число Эйлера (2,718…), основание натурального логарифма.

Возвращает , из которого вычли единицу.

Возвращает значение числа, округлённое к меньшему целому.

Возвращает ближайшее число с плавающей запятой одинарной точности, представляющие это число.

Возвращает квадратный корень из суммы квадратов своих аргументов.

Возвращает результат умножения 32-битных целых чисел.

Возвращает натуральный логарифм числа (log_e, также известен как ln).

Возвращает десятичный логарифм числа.

Возвращает двоичный логарифм числа.

Возвращает наибольшее число из своих аргументов.

Возвращает наименьшее число из своих аргументов.

Возвращает основание в степени экспоненты, то есть, значение выражения .

Возвращает псевдослучайное число в диапазоне от 0 до 1.

Возвращает значение числа, округлённое до ближайшего целого.

Возвращает знак числа, указывающий, является ли число положительным, отрицательным или нулём.

Возвращает синус числа.

Возвращает гиперболический синус числа.

Возвращает положительный квадратный корень числа.

Возвращает тангенс числа.

Возвращает гиперболический тангенс числа.

Возвращает строку .

Возвращает целую часть числа, убирая дробные цифры.

Сравнение чисел

Как в word посчитать количество знаков

Для сравнения чисел в JavaScript используются следующие операторы: == (равно), != (не равно), > (больше), = (больше или равно),

Например, сравним два числа:

Console.log(2>3); //false
console.log(5>=3); //true

При сравнении чисел с дробной частью необходимо учитывать погрешности, которые могут возникать во время этих вычислений.

Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:

Console.log((0.2+0.4)==0.6); //false

Погрешности происходят потому что все вычисления компьютер или другое электронное устройство производит в 2 системе счисления. Т.е. перед тем как выполнить какие-то действия компьютер сначала должен преобразовать представленные в выражении числа в 2 систему счисления. Но, не любое дробное десятичное число можно представить в 2 системе счисления точно.

Например, число 0.25 10 в двоичную систему преобразуется точно.

0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1
0.125 10 = 0.001 2

Например, число 0.2 10 можно преобразовать в 2 систему только с определённой точностью:

0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
…
0.2 10 = 0.001100110011… 2

В результате эти погрешности скажутся при вычисления суммы двух чисел и результатах сравнения. Т.е. получится что на самом деле JavaScript будет видет эту запись следующим образом:

0.6000000000000001==0.6

При вычислениях или отображении чисел с дробной частью необходимо всегда указывать точность, с которой это необходимо делать.

Например, сравнить числа до 2 знаков после запятой используя методы toFixed() и toPrecision() :

//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true

Основные математические операции

В JavaScript существуют следующие математические операторы: + (сложение), — (вычитание), * (умножение), / (деление), % (остаток от деления), ++ (увелить значение на 1), — (уменьшить значение на 1).

6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x—); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(—x); //устанавливает 4 и выводит
Кроме этого в JavaScript есть комбинированные операторы: x+=y (x=x+y), x-=y (x=x-y), x*=y (x=x*y), x/=y (x=x/y), x%=y (x=x%y).
x = 3;
y = 6;
x+=y;
console.log(x); //9
x = 3;
y = 6;
x-=y;
console.log(x); //-3
x = 3;
y = 6;
x*=y;
console.log(x); //18
x = 3;
y = 6;
x/=y;
console.log(x); //0.5
x = 3;
y = 6;
x%=y;
console.log(x); //3

Сравнение чисел

Постановка знаков препинания в различных случаях. тире

Для сравнения чисел в JavaScript используются следующие операторы: (равно), (не равно), (больше), (меньше), (больше или равно), (меньше или равно).

Например, сравним два числа:

console.log(2>3); //false
console.log(5>=3); //true

Например, в JavaScript сумма чисел (0.2 + 0.4) не равна 0.6:

console.log((0.2+0.4)==0.6); //false

Например, число 0.25₁₀ в двоичную систему преобразуется точно.

0.125 × 2 = 0.25 | 0
0.25 × 2 = 0.5 | 0
0.5 × 2 = 1 | 1

0.125₁₀ = 0.001₂

Например, число 0.2₁₀ можно преобразовать в 2 систему только с определённой точностью:

0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
0.2 × 2 = 0.4 | 0
0.4 × 2 = 0.8 | 0
0.8 × 2 = 1.6 | 1
0.6 × 2 = 1.2 | 1
...

0.2₁₀ = 0.001100110011...₂

0.6000000000000001==0.6

Например, сравнить числа до 2 знаков после запятой используя методы и :

//метод toFixed()
console.log((0.2+0.4).toFixed(2)==(0.6).toFixed(2)); //true
//метод toPrecision()
console.log((0.2+0.4).toPrecision(2)==(0.6).toPrecision(2)); //true

Основные математические операции

В JavaScript существуют следующие математические операторы: (сложение), (вычитание), (умножение), (деление), (остаток от деления), (увелить значение на 1), (уменьшить значение на 1).

6+3 //9
6-3 //3
6*3 //18
6/3 //2
6%3 //0, т.е. 6:3=2 => 6-3*2 => ост(0)
5%2 //1, т.е. 5:2=2(.5) => 5-2*2 => ост(1)
7.3%2 //1.3, т.е. 7.3:2=3(.65) => 7.3-2*3 => ост(1.3)
//знак результата операции % равен знаку первого значения
-9%2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-9%-2.5 //-1.5, т.е. 9:2.5=3(.6) => 9-2.5*3 => ост(1.5)
-2%5 //-2, т.е. 2:5=0(.4) => 2-5*0 => ост(2)
x = 3;
console.log(x++); //выводит 3, у уже потом устанавливает 4
console.log(x); //4
x = 3;
console.log(++x); //устанавливает 4 и выводит
x = 5;
console.log(x--); //выводит 5, у уже потом устанавливает 4
console.log(x); //4
x = 5;
console.log(--x); //устанавливает 4 и выводит

Description

If the fractional portion of the argument is greater than 0.5, the argument is rounded to the integer with the next higher absolute value. If it is less than 0.5, the argument is rounded to the integer with the lower absolute value. If the fractional portion is exactly 0.5, the argument is rounded to the next integer in the direction of +∞. Note that this differs from many languages» round() functions, which often round this case to the next integer away from zero

, instead giving a different result in the case of negative numbers with a fractional part of exactly 0.5.

Because round() is a static method of Math , you always use it as Math.round() , rather than as a method of a Math object you created (Math has no constructor).

Как проверить является ли переменная числом

Определить является ли значение переменной числом можно используя один из следующих способов:

1. С использованием функций isNaN и isFinite:

// myVar — переменная
if (!isNaN(parseFloat(myVar)) && isFinite(parseFloat(myVar))) {
//myVar — это число или может быть приведено к нему
};

В виде функции:

// функция
function isNumeric(value) {
return !isNaN(parseFloat(value)) && isFinite(parseFloat(value));
}
// использование
var myVar = «12px»;
console.log(isNumeric(myVar)); //true

Этот способ позволяет определить является ли указанное значение числом или может быть приведено к нему. Данный вариант не считает числом пустую строку, строку из пробелов, значение null , Infinity , -Infinity , true и false .

2. С использованием оператора typeof и функций isFinite, isNaN:

// функция которая проверяет является ли значение числом
function isNumber(value) {
return typeof value === «number» &&
isFinite(value) &&
!isNaN(value);
};
// использование функции isNumber
isNumber(18); //true
// использование функций для проверки текстовых значений
isNumber(parseFloat(«»)); //false
isNumber(parseFloat(«Infinity»)); //false
isNumber(parseFloat(«12px»)); //true

Эта функция определяет имеет ли указанное значение тип Number, а также не принадлежит ли оно к одному из специальных значений Infinity, -Infinity и NaN. Эсли это так, то данная функция возвращает значение true.

3. С помощью метода ECMAScript 6 Number.isInteger(value) . Данный метод позволяет определить, является ли указанное значение целым числом.

Number.isInteger(«20»); //false, т.к. данный метод не выполняет перевод строки в число
Number.isInteger(20); //true, т.к. данное значение является числом

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

let billion = 1000000000;

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как “1млрд” или “7.3млрд” для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву “e”, чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

let billion = 1e9; // 1 миллиард, буквально: 1 и 9 нулейalert( 7.3e9 ); // 7.3 миллиардов (7,300,000,000)

Другими словами, “e” производит операцию умножения числа на 1 с указанным количеством нулей.

1e3 = 1 * 10001.23e6 = 1.23 * 1000000

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет “e”.

let ms = 1e-6; // шесть нулей, слева от 1

Если мы подсчитаем количество нулей 0.000001, их будет 6. Естественно, верная запись 1e-6.

Другими словами, отрицательное число после “e” подразумевает деление на 1 с указанным количеством нулей:

// 1 делится на 1 с 3 нулями1e-3 = 1 / 1000 (=0.001)// 1.23 делится на 1 с 6 нулями1.23e-6 = 1.23 / 1000000 (=0.00000123)

Шестнадцатеричные, двоичные и восьмеричные числа

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: 0x, после которого указывается число.

Например:

alert( 0xff ); // 255alert( 0xFF ); // 255 (то же самое, регистр не имеет значения)

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются 0b для двоичных и 0o для восьмеричных:

let a = 0b11111111; // бинарная форма записи числа 255let b = 0o377; // восьмеричная форма записи числа 255alert( a == b ); // true, с двух сторон число 255

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию parseInt (рассмотрим позже в этой главе).

Как явно преобразовать строку в число?

Явно привести строку в число можно посредством следующих способов:

1. Использовать унарный оператор + , который необходимо поместить перед значением.

Этот способ пренебрегает пробелами в начале и конце строки, а также \n (переводом строки).

Используя данный способ необходимо обратить внимание на то, что пустая строка или строка, состоящая из пробелов и \n , переводится в число 0. Кроме этого она также преобразует тип данных null и логические значения к числу

2. Функция parseInt . Данная функция предназначена для преобразования аргумента в целое число . В отличие от использования унарного оператора + , данный метод позволяет преобразовать строку в число, в которой не все символы являются цифровыми . Начинает она преобразовывать строку, начиная с первого символа. И как только она встречает символ, не являющийся цифровым, данная функция останавливает свою работу и возвращает полученное число.

Данная функция может работать с разными системами счисления (двоичной, восьмеричной, десятичной, шестнадцатеричной). Указание основание системы счисления осуществляется посредством 2 аргумента.

Кроме этого рекомендуется, всегда указывать основание системы счисления и не полагаться на значение по умолчанию установленное этой функции, например в том или ином браузере.

Кроме функции parseInt в JavaScript имеется метод Number.parseInt . Данный метод ничем не отличается от функции parseInt и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

3. Функция parseFloat . Функция parseFloat аналогична parseInt , за исключением того что позволяет выполнить преобразование аргумента в дробное число.

Кроме этого функция parseFloat в отличие от parseInt не имеет 2 аргумента, и следовательно она всегда пытается рассмотреть строку как число в десятичной системе счисления.

Кроме функции parseFloat в JavaScript имеется метод Number.parseFloat . Данный метод ничем не отличается от функции parseFloat и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

Примеры

Пример: использование метода Math.ceil()

Следующий пример показывает использование метода Math.ceil().

Math.ceil(.95); // 1Math.ceil(4); // 4Math.ceil(7.004); // 8Math.ceil(-0.95); // -0Math.ceil(-4); // -4Math.ceil(-7.004); // -7

Пример: корректировка округления десятичных дробей

Rounding the Number

Whatever your reason for rounding numbers may be, JavaScript has
several ways of allowing you to round numbers. Let us look at the most
common ones.

Rounding to the Nearest Integer

The most common function for rounding your value is the prom king
himself, Math.round:

Math.round(1.532); // 2
Math.round(1.235); // 1
Math.round(27.94); // 28
Math.round(0.0005); // 0

This function works by rounding your number to the nearest integer.
If the first number after the decimal is 5 or higher, it rounds up. If
the first number after the decimal is 4 or lower, it rounds down. The
Math.round function most closely
resembles what you may have learned in school.

Its equally popular variants are the
Math.floor and
Math.ceil functions. Whereas Math.round
would either round up or down depending on what the number after the
decimal is, Math.floor will always round
down to the next lowest integer regardless of what the value after the
decimal is. Similarly…in an opposite way,
Math.ceil will always round up to the next highest integer
regardless of what the value after the decimal actually is:

Math.ceil(1.5); // 2
Math.floor(1.5); // 1
Math.floor(1.235); // 1
Math.ceil(0.0005); // 1

All of this should look pretty straightforward. Just to drive the point
home about the next highest and lowest integers, let’s look what happens
when we are dealing with negative values:

Math.ceil(-45) // -45
Math.floor(-45) // -45
Math.ceil(-.5) // 0
Math.floor(-.5) // -1
Math.round(-45) // -45
Math.round(-.5) // -1
Math.round(-1.24) // -1

The Math.ceil and
Math.floor functions work as expected.
They round up or down to the next largest or smallest integer. Remember,
in the negative world, the smaller the absolute value of your number,
the larger its actual value:

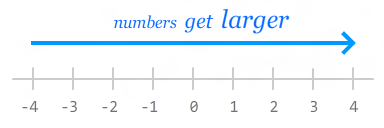
That is why rounding up from -.5
results in you getting . If you think
of the relative size of numbers as being on the number line,
Math.ceil goes right.
Math.floor goes left. It’s like opposite day over there.

Our prom king Math.round, though,
exhibits some slightly shallow behavior. Instead of rounding up or down
to the nearest large or small number, this function literally rounds up or
rounds down based on the absolute value of the number. That is why
rounding -.5 is actually a
-1 (a smaller number) than being 0 like
you may expect.

Rounding to Arbitrary Levels of Precision

In the previous section, you learned how you can round to the nearest
integer. There will be times when you want to round to a particular
decimal position for extra preciseness. Let’s say we want to round our value of Pi to just 2 digits past the
decimal point. In other words, we want 3.14159
to be rounded off to 3.14. Using the
three amigos (Math.round,
Math.floor, and
Math.ceil) without any modification will cause our value to either
be 3 or 4. That’s not what we want.

To get what we want, there is a simple approach we can take made up of just three steps:

To get X digits of precision, multiply our number by 10 to the power of X.
Round the result using Math.round()
Divide the new result by 10 to the power of X again.

To make this more concrete, let’s see we want to round 3.14159 to two digits of precision. To get two decimal positions of precision,
we can multiply our number by 10 to the power of two
(aka 100) and round that value:

Math.round(3.14159 * 100);

Next, divide the result of this rounding
operation by 10 to the power of two again to get
the answer you are looking for:

Math.round(3.14159 * 100) / 100; // result is 3.14

To generalize this a bit, here is a basic formula:

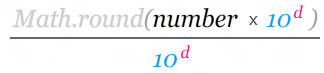
The d stands for the number of places after
the decimal point you want to go to. The number
is the value you are trying to round. Everything else should be
self-explanatory.

Using this model, here is how we can round 3.14159 to the tenths,
hundredths, thousandths, and ten thousandths positions:

Math.round(3.14159 * 10) / 10; // 3.1
Math.round(3.14159 * 100) / 100; // 3.14
Math.round(3.14159 * 1000) / 1000; // 3.142
Math.round(3.14159 * 10000) / 10000; // 3.1416

You can substitute Math.round with
Math.floor or
Math.ceil depending on what exactly you are going for, and the
behavior will be predictable.

Round() в Go 1.10

Для тех, кто не знаком с устройством float (я в их числе), этот код выглядит совершенно непонятно. Попробуем разобраться, что же он делает:

Похоже, что мы берём битовое представление числа, сдвигаем его и применяем маску. Согласно :

Рассматривая приведённые выше константы, мы видим, что сдвиг составляет 64 — 11 — 1, что означает 64 бита на число, 11 из которых используются для показателя степени, один — для знака и 52 оставшихся бита — для мантиссы. Это означает, что используемый сдвиг удаляет биты мантиссы, а маска удаляет бит знака, оставляя нас только с показателем степени.

В полученном числе показатель степени записан не как он есть, а с прибавлением числа 1023 (это делается для того чтобы записывать отрицательные показатели для очень маленьких чисел), что означает, что мы должны вычесть 1023 из e, вычисленного выше, чтобы получить фактический показатель. Иными словами, если e < bias, то мы имеем отрицательный показатель степени, что означает, что абсолютное значение float должно быть < 1. Действительно, дальше мы видим:

Здесь бит маскируется знаковым битом, это используется только для сохранения правильного знака: теперь мы можем полностью игнорировать мантиссу. Мы можем это сделать, потому что в этом случае нас интересует только показатель степени. Так как используется основание степени 2, а e < bias, мы знаем, что наименьший показатель, который может быть, равен -1, а 2 ^ -1 = 0,5. Кроме того, мантисса имеет некоторое значение 1.X. Таким образом, в зависимости от показателя наше число находится либо в диапазоне (0,5, 1), либо в диапазоне (0, 0,5). Поэтому во втором случае для правильного округления нам нужно добавить к числу единицу. Фух. Подробнее это описано в википедии.

Теперь разберём второй случай:

Наверное, вы думаете, что условие в этой ветке должно быть e > bias, чтобы покрыть все случаи с положительным показателем степени. Но вместо этого тут используется только их часть. Использование сдвига здесь особенно интересно, потому что кажется, что оно несравнимо с bias. Первое — это число битов смещения, а второе — численное смещение. Но, поскольку числа с плавающей точкой представлены как (1.мантисса) * 2 ^ X, то если X больше числа битов в мантиссе, мы гарантированно получим значение без дробной части. То есть показатель степени сместил десятичную точку вправо настолько, что мантисса окончательно пропала. Таким образом, выражение в этой ветке игнорирует числа с плавающей точкой, которые уже округлены.

Первая строка тут простая: вычитаем bias из e и получаем реальное значение показателя степени. Вторая строка добавляет к значению 0,5. Это работает, потому что старший бит мантиссы добавляет 0,5 к финальной сумме (см. представление в статье “Википедии” ниже). В этом случае эта сумма переполняет 52-битные границы мантиссы, показатель степени будет увеличен на 1. Значение показателя степени не сможет переполниться до знакового бита, так как оно не может быть больше bias+shift из примера выше. В любом случае, дробная часть очищается. Таким образом, если дробная часть была больше или равна 0,5, она будет увеличена на 1, в противном случае будет отброшена. Хитро и не очевидно до тех пор, пока мы не посмотрим глубже.

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Привязка к диапазону

Иногда нужно получить значение х, которое должно находиться в пределах определенного диапазона. Например, нужно значение от 1 до 100, но мы получаем значение 123. Чтобы исправить это, можно использовать min() (возвращает наименьшее из чисел) и max (возвращает максимально допустимое число).

Использование:

var lowBound = 1;
var highBound = 100;
var numInput = 123;
var clamped = Math.max(lowBound, Math.min(numInput, highBound));
console.log(clamped);
> 100;

Можно создать функцию или расширение класса Number:

Number.prototype.clamp = function(min, max) {
  return Math.min(Math.max(this, min), max);
};

Использование:

(numInput).clamp(lowBound, highBound);

8 ответов:

вы должны преобразовать свой ввод в число, а затем вокруг них:

или как один лайнер:

тестирование с разными значениями:

Если вам нужно округлить до определенного количества цифр использовать следующие функции

по словам спецификация ECMAScript, числа в JavaScript представлены только 64-разрядным форматом двойной точности IEEE 754. Следовательно, в JavaScript на самом деле нет целочисленного типа.

Что касается округления чисел, есть несколько способов, вы можете достичь этого. Элемент мат объект дает нам три метода округления, которые мы можем использовать:

The математика.круглый () наиболее часто используется, он возвращает значение округляется до ближайшего целого числа. То есть математика.этаж() который возвращает наибольшее целое число, меньшее или равное числу. Наконец у нас есть математика.ceil () функция, которая возвращает наименьшее целое, большее или равное количеству.

есть еще toFixed(), который возвращает строку, представляющую число с фиксированной точкой.

Ps.: Есть нет 2-й аргумент в математика.круглый () метод. Элемент toFixed() и не то есть конкретный, его внутри спецификация ECMAScript также

вот способ, чтобы иметь возможность использовать Math.round() со вторым аргументом (количество десятичных знаков для округления):

вы также можете использовать toFixed(x) или toPrecision(x) здесь x — количество цифр.

оба эти метода поддерживаются во всех основных браузерах

можно использовать математика.круглый () для округления чисел до ближайшего целого числа.

кроме того, вы можете использовать parseInt() и parseFloat() для приведения переменной к определенному типу, в этом случае целочисленный и с плавающей точкой.

очень хорошее приближение для округления:

только в некоторых случаях, когда длина десятичной части числа очень длинная, это будет неверно.

Округление в большую сторону до ближайшего целого числа

Если вы хотите округлить десятичные числа вверх, используйте Math.ceil. Действие этого метода также можно представить, как бесконечный лифт: Math.ceil всегда везет вас «вверх«, независимо от того, является ли число отрицательным или положительным:

Math.ceil(42.23);
> 43
Math.ceil(36.93);
> 37 
Math.ceil(-36.93); -36

Округление до ближайшего кратного числа

Если нужно округлить значение до ближайшего числа, кратного 5, создайте функцию, которая делит число на 5, округляет его, а затем умножает результат на то же значение:

function roundTo5(num) {
    return Math.round(num/5)*5;
}

Использование:

roundTo5(11);
> 10

Если нужно выполнить JavaScript округление до двух знаков, можно передавать функции, как начальное число, так и кратность:

function roundToMultiple(num, multiple) {
    return Math.round(num/multiple)*multiple;
}

Чтобы использовать функцию, включите в ее вызов округляемое число и кратность:

var initialNumber = 11;
var multiple = 10;
roundToMultiple(initialNumber, multiple);
> 10;

Чтобы округлять значения только в большую или меньшую сторону замените в функции round на ceil или floor.