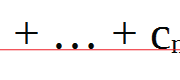Сетевой график: пример построения

Алгоритм построения сетевого графика

Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.

Шаг 1. Определить основную цель проекта

Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.

Шаг 2. Выявить ограничения

Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.

Шаг 4. Оценить длительность работ

Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.

Шаг 5. Определить последовательность работ

Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.

Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.

Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.

Шаг 6. Указать связи между работами

Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.

Шаг 7. Определить раннее начало и раннее окончание

Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.

Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.

Шаг 8. Определить поздние начало и окончание

Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.

Шаг 9. Определить временной резерв

Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.

Шаг 10. Выявить критический путь

Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.

Метод сетевого моделирования

Сетевое планирование и управление получило активное развитие с 50-х годов прошлого века сначала в США, затем в других развитых странах и в СССР. Такие методы сетевого планирования, как CPM, PERT позволили существенно поднять «планку» проектного управления в направлении оптимизации временных и содержательных параметров графиков работ. Это дало возможность разрабатывать расписания проектных задач на основе более эффективной методологии сетевого моделирования, вобравшей в себя весь лучший опыт (схема методов календарного планирования приведена ниже). Сетевая диаграмма имеет различные названия, среди них:

• сетевой график;
• сетевая модель;
• сеть;
• граф сети;
• стрелочная диаграмма;
• PERT-диаграмма, и т.д.

Визуально сетевая модель проекта представляет собой графическую схему последовательного комплекса работ и связей между ними. Стоит заметить, что система планирования и управления проектом целостно отображается в графической форме состава операций, их временных протяженностей и взаимосвязанных событий. Основой метода построения модели служит раздел математики, именуемый теорией графов, сформировавшийся в начале 50-х – конце 60-х годов.

Методы календарного планирования и управления проектам

В модели сетевого планирования и управления под графом понимается геометрическая фигура, включающая бесконечное или конечное множество точек и линий, соединяющих между собой эти линии. Граничные точки графа называют его вершинами, а ориентированные в направлениях соединяющие их точки – ребрами или дугами. Сетевая модель в свой состав включает именно ориентированные графы.

Вид ориентированного графа

Разберем другие основные понятия сетевой модели проекта.

Работа – часть производственного или проектного процесса, имеющая начало и окончание в форме количественно описываемого результата, требующая затрат времени и других ресурсов. Работа отражается на диаграмме в форме однонаправленной стрелочной линии. Формой работ мы можем считать операции, мероприятия и действия.

Событие – факт завершения работ, результат которых необходим и достаточен для начала реализации следующих операций

Вид события на модели отражается в форме кружков, ромбиков (вехи) или других фигур, внутри которых помещается идентификационный номер события.

Веха представляет собой работу с нулевой продолжительностью и обозначает важное, значимое событие в проекте (например, утверждение или подписание документа, акт окончания или начала проектного этапа и т.п.).

Ожидание – это процедура, которая не потребляет никаких ресурсов, кроме затрат времени. Отображается как линия со стрелкой на конце с отметкой длительности и указанием наименования ожидания.

Фиктивная работа или зависимость – вид технологической и организационной связи работ, не требует никаких усилий и ресурсов, в том числе затрат времени

На сетевой диаграмме показывается как пунктирная стрелка.

Решение задач сетевого планирования

Срок выполнения	от 1 дня
Цена	от 100 руб./задача
Предоплата	50 %
Кто будет выполнять?	преподаватель или аспирант

УЗНАТЬ СТОИМОСТЬ РАБОТЫ ПО СЕТЕВОМУ ПЛАНИРОВАНИЮ

Решение задач сетевого планирования студенты изучают на различных дисциплинах, связанных с теорией графов и методами оптимального решения. В данной статье будут рассмотрены два примера решения таких задач. Мы постараемся не использовать сложных и запутанных формул, чтобы показать, как на самом деле всё просто.

Суть задачи

 Задачи сетевого планирования сводятся к двум целям:

1. Найти оптимальный маршрут;
2. Определить, как максимально быстро выполнить проект.

 В первом случае рассматриваются такие случаи, когда необходимо соединить несколько независимых узлов, находящихся в одной сети. Сделать это необходимо максимально коротким способом.

Например, в некотором районе города требуется провести трубопровод к нескольким домам. Понятно, что к разным домам могут вести несколько дорог.

Таким образом, нам нужно определить, какой из маршрутов прокладки будет наиболее коротким. Узлами в этом случае будут наши дома.

Во втором случае задачи предполагают, что существует некий проект, который состоит из нескольких работ. Работы могут выполняться поочередно, друг за другом, но не каждая из них для начала выполнения требует завершения какой-то из предыдущих работ.

Соответственно, обе задачи решаются с помощью графов – точек, соединенных между собой произвольными линиями.

В задаче первого типа граф даётся, как правило, условием задачи, а во втором случае его необходимо изобразить самостоятельно. Этим мы сейчас и займёмся.

Первый случай

  Выше вы видите граф. Цифры в кружках – это дома, к которым телевизионная компания планирует подвести кабеля. Как мы видим, к одному кружку могут вести два или три пути. Пути называются рёбрами графа. У каждого пути есть свой вес. Это наше расстояние.

Нам нужно выбрать из всего этого обилия путей самый короткий, который объединит каждый кружок – вершину графа. Для этой цели существует специальный алгоритм «Прима». Его суть заключается в следующем: Мы начинаем идти из первой вершины и присоединяем к ней ребро, имеющее самый маленький вес. В нашем случае – это ребро 1;2.

Его вес равен 1. Теперь мы присоединяем самое короткое ребро, из всех выходящих из вершин 1 и 2. Это ребро 2;5. Его вес – 3. У нас уже три вершины – 1,2,5. Присоединяем самое короткое ребро, выходящее из них. И это – 2;4. Его вес – 4. Самое короткое ребро, выходящее из вершин 1,2,4,5 – 4;6. Оно равно 3. Последнее ребро – 4;3.

Мы объединили все вершины. Наш путь в сумме составляет: 1 + 3 + 4 + 3 + 5 = 16.  

Второй случай

 Здесь всё немного сложнее, чем в вышеописанном примере. По условию даётся таблица примерно следующего характера.   На основании данной таблицы мы рисуем следующий граф.

  Правила при составлении графа простые: Каждая следующая работа всегда находится правее предшествующей. 

Никакая работа не может быть начата без выполнения всех предыдущих по условию.

Мы не могли бы начать делать b10, не сделав b3, выполнение которой приходится на вершину 3. Мы не можем строить стены, не возведя фундамент.

Тупиков быть не должно. Из каждой вершины выходит как минимум, одно ребро. Далее мы находим так называемый «критический путь». Это самое длинное расстояние от 0 до 6. Мы начинаем двигаться из нуля и присоединяем каждую вершину самым длинным путём. Например, 3 мы можем присоединить, пройдя ребро 0;3, вес которого – 8 или два ребра – 0;1 и 1;3, а так же 0;2 и 2;3.

Обратите внимание, что ребро 3;5 имеет нулевой вес, поэтому и кратчайший путь к вершине 3 будет равен 12. Подпишем самые короткие пути снизу вершин

  Там, где разница между самым коротким и самым длинным путём будет равна нулю, проходит критический путь. На рисунке ниже он подчёркнут двойными чертами.   

Это крайний срок выполнения проекта. Он равен 3 + 9 + 7 = 19.

Раньше этого успеть нельзя. По остальным работам есть резерв времени. Чтобы его посчитать, отнимите верхнее число от нижнего над каждой вершиной.

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Сетевой график — инструмент оптимизации деятельности фирмы

Когда речь заходит об использовании ресурсов (в том числе и трудовых), руководителю гораздо проще ими распоряжаться, если есть сетевой график производства работ. На нем видны все простои и занятость каждого конкретного сотрудника (бригады). Использование не занятого работника на одном объекте для реализации другого позволяет оптимизировать деятельность компании в целом.

Не стоит пренебрегать и еще одним практическим советом. В реальности руководители проектов сталкиваются с «желаниями вышестоящего руководства» видеть работу выполненной «вчера». Для того чтобы избежать паники и выпуска брака, необходимо усиливать ресурсы не столько на операциях критического пути, сколько на непосредственно влияющих на него. Почему? Да потому, что на критическом пути и так нет простоев, и сокращать время производства работ зачастую невозможно.

Использование табличного метода

Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.

Модель расчета параметров сетевого графика табличным способом

Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.

1. Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
2. Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
3. Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
4. Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.

Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.

Выбор типа отображаемых сведений о задаче

Если некоторые элементы отображаются ненужным образом (или вы запускаете перегрузку данных), попробуйте изменить сведения о задаче в каждом поле, чтобы увидеть только наиболее важные данные.

Выберите команду Просмотреть схему сети_гт_.

Выберите Формат _Гт_ных полей.

В списке Параметры стиля для выберите задачу, которую вы хотите изменить.

В разделе границавыберите параметры фигуры, цвет, ширина и линии сетки, чтобы создать нужный внешний вид.

Выберите имя в разделе шаблон данных , чтобы применить изменения к существующему шаблону. Чтобы создать новый шаблон, который будет использовать ваши изменения, выберите пункт Дополнительные шаблоныи нажмите кнопку создать (чтобы создать новый шаблон), Копировать (чтобы основать новый шаблон на существующем), изменить (для изменения шаблона) или импортировать (на Импорт шаблона из другого проекта.

Программы для создания сетевых диаграмм

Как мы уже сказали, мы собираемся показать несколько бесплатных инструментов для создания сетевой диаграммы и визуального управления нашими командами. Это предназначено для тех, у кого есть несколько серверов, подключенных к сети компьютеров.

Сетевой блокнот

Один из этих инструментов, который мы можем использовать, это Cеть Блокнот . Он имеет большое количество значков, поэтому мы можем создать нашу сеть визуально, всегда имея в виду все. Мы можем найти такие значки, как маршрутизаторы, принтеры, компьютеры, серверы, коммутаторы…

С помощью сетевого блокнота мы можем проектировать нашу сеть . Очень интересно для организации, которая хочет создать сетевую диаграмму, показывающую все компоненты, такие как точки доступа, компьютеры, подключенные принтеры… Короче говоря, все компьютеры, составляющие эту сеть.

к скачать этот инструмент мы можем перейти на его веб-сайт. Там мы найдем разные версии. Кроме того, нам нужно будет загрузить пакет с более чем 100 значками, которые мы можем использовать для создания нашей сетевой диаграммы.

Netpict

Еще один очень интересный инструмент, который мы можем использовать для наших целей: Netpict . Однажды мы скачать и установив программу, мы увидим различные значки, относящиеся к имеющимся у нее сетям. У нас есть маршрутизатор, коммутатор, сервер, облако, беспроводная связь…

Его интерфейс очень прост в использовании. Мы можем создавать наши диаграммы как захотим. Вам просто нужно взять значки слева и переместить их на панель.

NetProbe

Этот инструмент не только позволяет создавать сетевые диаграммы, но и имеет функцию сканирования сети. Мы можем добавить для него диапазон IP-адресов и маску сети.

NetProbe позволяет нарисовать схему сети и настроить ее так, как нам нужно, как и в предыдущих случаях.

ДиаграммаДизайнер

Еще один инструмент, который мы хотим показать: ДиаграммаДизайнер . Это открытый исходный код, который позволяет нам создавать сетевые диаграммы с самых основ. Это простое программное обеспечение, хотя дизайн старый. Он совместим с разными версиями Windows.

Однажды мы скачать и установите его, операция такая же, как и в предыдущих случаях. Мы можем выбрать значки, которые соответствуют тому, что нам нужно, и нарисовать сетевую диаграмму по своему усмотрению.

Вкратце, это некоторые варианты создания сетевых диаграмм. Если вам нужно управлять бизнесом, большим помещением, где много сетевых команд, хорошей идеей будет создание диаграммы. Таким образом, мы можем иметь больший контроль, правильно управлять всем, что нам понадобится, а также иметь возможность решать возможные проблемы, которые могут возникнуть. Мы видели различные инструменты, которые есть в нашем распоряжении бесплатно и для Windows, которая сегодня является наиболее часто используемой операционной системой на настольных компьютерах.

Пример сети с использованием программного обеспечения Visual Paradigm

Теперь пришло время создать нашу небольшую сеть с помощью сетевой диаграммы Visual Paradigm. Мы начнем с очень краткого объяснения кнопок вверху справа, где мы будем строить нашу сеть.

Здесь со стрелками, которые у нас есть влево и вправо, мы можем вернуться и продвинуться в действиях, которые мы сделали. Что еще мы можем сделать:

• Поместите цвет заливки, цвет линии, тень и отформатируйте копию.
• Установите соединительные линии и ориентиры.

Если вы аккуратно наводите курсор на каждую кнопку, прокомментируйте, для чего она предназначена. Теперь мы начнем создавать нашу сеть, слева мы выберем маршрутизатор и ПК, щелкнув по ним. Мы также вставим текст, чтобы лучше идентифицировать устройства. Чтобы поместить текст, мы можем сделать это под значками в Общие или в верхнем меню Вставить Текст .

Тогда мы получим такой результат:

Следующим шагом является щелчок по маршрутизатору, чтобы установить линию соединения между маршрутизатором WiFi и ПК Луиса. Там мы увидим четыре большие стрелки, где мы сможем выбрать ту, которая нам больше всего подходит. Тот, который я использовал для этого урока, я обозначил другой стрелкой.

Затем, когда мы связываемся со второй командой, мы можем выбрать тип соединения, которое хотим создать, в этом случае мы установили двунаправленное соединение.

Это будет окончательный результат подключения:

Теперь я собираюсь создать пример с сетью из 3 ПК, маршрутизатора WiFi, смартфона и принтера.

Как видите, сетевая диаграмма Visual Paradigm позволяет нам создавать наши сетевые диаграммы. Тогда его сложность будет зависеть от того, поставите ли вы в свою сеть больше оборудования.