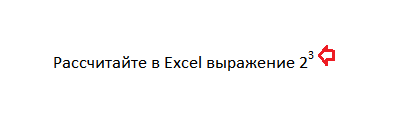Округление чисел в excel в большую и меньшую сторону

Функция SQL ROUND

Функция SQL ROUND(результат_вычислений, n) округляет результат вычислений до n-го знака после запятой.
Округление производится по правилам арифметики.

Если n — отрицательное число (−n), то округление происходит до n-го знака перед запятой. Таким образом,
с помощью функции ROUND можно получить и целое число как результат округления.

Пример 1. В базе данных фирмы есть таблица Staff, содержащая
данные о сотрудниках фирмы. Выведем индивидуальные размеры заработной платы сотрудников:

SELECT Name, Salary
FROM STAFF

Результатом выполнения запроса будет следующая таблица:

Name	Salary
Sanders	18357.5
Pernal	15430.0
Marenghi	17506.8
Doctor	12322.8
Factor	16228.7
Junkers	16232.8
Moonlight	21500.6
Aisen	19540.7
MacGregor	15790.8

Для вычисления среднего размера заработной платы пишем запрос:

SELECT AVG(Salary)
FROM STAFF

Получим следующий результат:

AVG(Salary)

16990.06662326389

Для отчётов результат с таким числом знаков после запятой не годится. Округлим результат до второго
знака после запятой с помощью функции ROUND:

SELECT ROUND(AVG(Salary),2)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990.07

Пример 2. Теперь округлим результат до первого знака до запятой,
применяя в функции ROUND параметр минус единица:

SELECT ROUND(AVG(Salary),−1)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990

Сместим округление ещё на один знак влево и применим в функции ROUND параметр минус 2:

SELECT ROUND(AVG(Salary),−2)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

17000

Функция SQL ROUND может применяться ещё и с третьим необязательными параметром
(кроме MySQL). Если этим параметром будет 1, то округление производиться не будет, просто в результате
будет оставлено столько знаков после запятой, сколько указано во втором параметре.

Пример 3. Оставить в результате вычислений средней заработной
платы два знака после запятой, не производя округления. Применяем функцию ROUND с тремя параметрами:

SELECT ROUND(AVG(Salary),2,1)
AS Avg_Salary
FROM STAFF

Результат будет следующим:

Avg_Salary

16990.06

Функция MySQL TRUNCATE

В MySQL аналогом разновидности функции ROUND без округления результата является функция TRUNCATE.
Она, как и ROUND в общем случае имеет два параметра: результат вычислений и число знаков после запятой.

Пример 4. Условие то же, что в примере 3, но в MySQL. Применяем
функцию TRUNCATE:

SELECT TRUNCATE(AVG(Salary),2)
AS Avg_Salary
FROM STAFF

Получим результат без округления, как в предыдущем примере:

Avg_Salary

16990.06

Округление при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах погрешности измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,40 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Округление рассчитанного значения погрешности

Обычно в окончательном значении рассчитанной погрешности оставляют только первые одну-две значащие цифры. По одному из применяемых правил, если значение погрешности начинается с цифр 1 или 2(по другому правилу — 1, 2 или 3), то в нём сохраняют две значащих цифры, в остальных случаях — одну, например: 0,13; 0,26; 0,3; 0,8. То есть каждая декада возможных значений округляемой погрешности разделена на две части. Недостаток этого правила состоит в том, что относительная погрешность округления изменяется значительным скачком при переходе от числа 0,29 к числу 0,3. Для устранения этого предлагается каждую декаду возможных значений погрешности делить на три части с менее резким изменением шага округления. Тогда ряд разрешённых к употреблению округлённых значений погрешности получает вид:

• 0,10; 0,12; 0,14; 0,16; 0,18;
• 0,20; 0,25; 0,30; 0,35; 0,40; 0,45;
• 0,5; 0,6; 0,7; 0,8; 0,9; 1,0.

Однако при использовании такого правила последние цифры самого результата, оставляемые после округления, также должны соответствовать приведённому ряду.

Пересчёт значений физических величин

Пересчёт значения физической величины из одной системы единиц в другую должен производиться с сохранением точности исходного значения. Для этого исходное значение в одних единицах следует умножить (разделить) на переводной коэффициент, часто содержащий большое количество значащих цифр, и округлить полученный результат до количества значащих цифр, обеспечивающего точность исходного значения. Например, при пересчёте значения силы 96,3 тс в значение, выраженное в килоньютонах (кН), следует умножить исходное значение на переводной коэффициент 9,80665 (1 тс = 9,80665 кН). В результате получается значение 944,380395 кН, которое необходимо округлить до трёх значащих цифр. Вместо 96,3 тс получаем 944 кН.

Привязка к диапазону

Иногда нужно получить значение х, которое должно находиться в пределах определенного диапазона. Например, нужно значение от 1 до 100, но мы получаем значение 123. Чтобы исправить это, можно использовать min() (возвращает наименьшее из чисел) и max (возвращает максимально допустимое число).

Использование:

var lowBound = 1;
var highBound = 100;
var numInput = 123;
var clamped = Math.max(lowBound, Math.min(numInput, highBound));
console.log(clamped);
> 100;

Можно создать функцию или расширение класса Number:

Number.prototype.clamp = function(min, max) {
  return Math.min(Math.max(this, min), max);
};

Использование:

(numInput).clamp(lowBound, highBound);

Точные правила округления чисел

При округлении десятичных дробей недостаточно просто отбросить цифры после округляемого разряда. Убедиться в этом можно на таком примере. Если в магазине куплено 2 кг 150 г конфет, то говорят, что приобретено около 2 кг сладостей. Если же вес составляет 2 кг 850 г, то производят округление в большую сторону, то есть около 3 кг. То есть видно, что иногда округляемый разряд изменен. Когда и как это проделывают, смогут ответить точные правила:

1. Если после округляемого разряда следует цифра 0, 1, 2, 3 или 4, то округляемый оставляют неизменным, а все последующие цифры отбрасываются.
2. Если после округляемого разряда следует цифра 5, 6, 7, 8 или 9, то округляемый увеличивают на единицу, а все последующие цифры также отбрасываются.

К примеру, как правильно дробь 7,41 приблизить к единицам. Определяют цифру, которая следует за разрядом. В данном случае это 4. Следовательно, согласно правилу, число 7 оставляют неизменным, а цифры 4 и 1 отбрасывают. То есть получаем 7.

Если округляется дробь 7,62, то после единиц следует цифра 6. Согласно правилу, 7 необходимо увеличить на 1, а цифры 6 и 2 отбросить. То есть в результате получится 8.

Представленные примеры показывают, как округлить десятичные дроби до единиц.

Приближение до целых

Отмечено, что округлять до единиц можно точно так же, как и до целых. Принцип один и тот же. Остановимся подробнее на округлении десятичных дробей до определенного разряда в целой части дроби. Представим пример приближения 756,247 до десятков. В разряде десятых располагается цифра 5. После округляемого разряда следует цифра 6. Следовательно, по правилам необходимо выполнить следующие шаги:

• округление в большую сторону десятков на единицу,
• в разряде единиц цифру 6 заменяют нулем,
• цифры в дробной части числа отбрасываются,
• в результате получают 760.

Обратим внимание на некоторые значения, в которых процесс математического округления до целых по правилам не отображает объективную картину. Если взять дробь 8,499, то, преобразовывая его по правилу, получаем 8

Но по сути это не совсем так. Если поразрядно округлить до целых, то вначале получим 8,5, а затем отбрасываем 5 после запятой, и осуществляем округление в большую сторону.

Получаем 9, что, в принципе, не сосем точно. То есть в таких значениях погрешность существенна. Поэтому оцениваем задачу и, если ситуация позволяет, то лучше использовать значение 8,5.

Приближение до десятых

Как округлить до десятых, до сотых, до тысячных? Операция осуществляется по таким же правилам, как и до целых. Основная задача – правильно определить округляемый разряд и знак, который следует за ним.

К примеру, дробь 6,7864 при доведении:

• до десятых становится равной 6,8,
• до сотых – 6,79,
• если округлить до тысячных, то получают 6,786.

Обратите внимание! Незнание этих правил очень удачно используют маркетологи. В магазинах, наблюдая ценник с указанием числа 5,99, большинством покупателей воспринимается цена, равная 5

В действительности же цена товара практически 6.

Математика учимся округлять числа

Правила округления чисел до десятых

Правила округления чисел

Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:

• Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
• Если цифра меньше 5, то значение округляют без увеличения.

Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.

Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.

Что мы узнали?

Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Настройка отображения чисел через панель инструментов

Самый простой способ округлить число, а точнее, его отображения на экране – через кнопки на Панели инструментов. Чтобы найти их, должна быть открыта вкладка “Главная”, в которой расположен подраздел “Число”. Здесь и находятся требуемые функции “Увеличить разрядность” или “Уменьшить разрядность”.

Выберите ячейку с числом и нажмите на кнопку с нужным действием. Функция “Увеличить разрядность” будет добавлять в конец дробной части нули.

Функция “Уменьшить разрядность” будет убирать цифры с конца, округляя окончания.

Примечание: Важно помнить, что числовое значение, которое хранится в памяти программы после проделанных действий никак не изменится, и расчеты будут производиться с исходным значением

Округление числа с помощью формата ячеек

Формат ячеек позволит выбрать необходимое количество цифр, которое должно отображаться в числе после запятой.

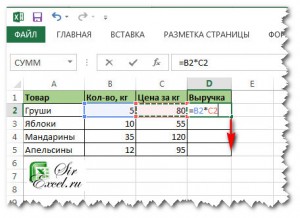
Округлять будем число 23,5168 в ячейке А1. Кликаем по нему правой кнопкой мыши и из контекстного меню выбираем «Формат ячеек».

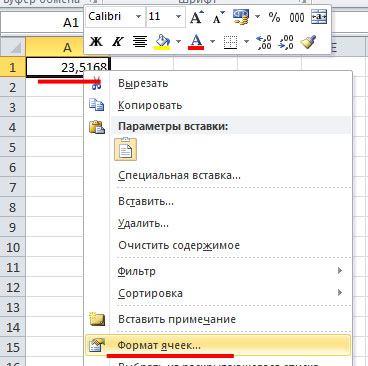
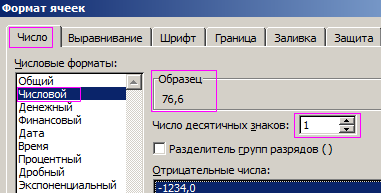
Дальше, на вкладке «Число» из списка «Числовые форматы» выберите «Числовой». В поле «Число десятичных знаков» поставьте нужное значение. Нажмите «ОК».

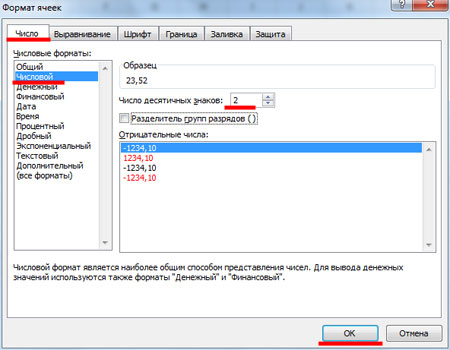
Количество знаков после запятой уменьшилось до 2-х. Как видите, округление числа происходит по математическим законам: если отбрасываемая цифра меньше пяти – число округляется в меньшую сторону, если больше пяти или равно – в большую.

Значение в ячейке изменилось только визуально. В строке формул по-прежнему стоит число 23,5168, и именно оно будет браться для любых расчетов, в которых будет указана ячейка А1.

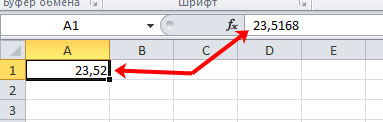
Чтобы уменьшить или увеличить количество знаков после запятой, можно использовать и следующий способ. На вкладке «Главная» в группе «Число» Вы найдете две кнопочки «Увеличить разрядность» и «Уменьшить разрядность».

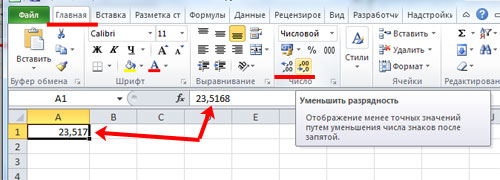
Выделим ячейку А1 и нажмем один раз на кнопку «Уменьшить разрядность». Получим вот такой результат.

Правила округления десятичной дроби

Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.

В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:

— Который час?

— Какой вес?

— Сколько стоит?

Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).

Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.

Число, полученное при округлении, называют приближенным значением данного числа.

Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.

Если число c < х < d, тогда с — это приближенное значение x с недостатком. А d — это приближенное значение x с избытком.

Чтобы округлить дробную часть десятичной дроби, пользуйтесь следующими правилами:

1. Подчеркните цифру округляемого разряда.
2. Отделите все цифры, стоящие справа.
3. Если справа от цифры, которую нужно округлить, стоит 0, 1, 2, 3 или 4 — цифра остается без изменений. Отбросьте все цифры справа от цифры округляемого разряда.
4. Если справа от цифры округляемого разряда стоит 5, 6, 7, 8 или 9 — к цифре округляемого разряда прибавляем один. Отбросьте все цифры справа.

Приближенное значение записывается после вот такого знака: ≈

Еще одно правило округления, которое нужно запомнить Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число. Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.

Получение приближенных значений

Это математическое действие осуществляется по определенным правилам.

Но для каждого множества чисел они разные. Отмечают, что округлить можно целые числа и десятичные дроби.

А вот с обыкновенными дробями действие не выполняется.

Сначала их необходимо перевести в десятичные дроби, а затем приступить к процедуре в необходимом контексте.

Правила приближения значений заключаются в следующем:

• для целых – замена разрядов, следующих за округляемым, нулями,
• для десятичных дробей – отбрасывания всех чисел, которые находятся за округляемым разрядом.

К примеру, округляя 303 434 до тысяч, необходимо заменить сотни, десятки и единицы нулями, то есть 303 000. В десятичных дробях 3,3333 округляя до десятых, просто отбрасывают все последующие цифры и получают результат 3,3.

Как округлить число до сотых

Правило округления числа до сотых

Чтобы округлить число до сотых, надо оставить после запятой две цифры, а остальные отбросить.

Если первая из отброшенных цифр 0, 1, 2, 3 или 4, то предыдущую цифру не изменяем.

Если первая из отброшенных цифр 5, 6, 7, 8 или 9, то предыдущую цифру увеличиваем на единицу.

Пример округления числа до сотых:

\ Чтобы округлить число до сотых, оставляем после запятой две цифры, а следующую за ними цифру отбрасываем. Поскольку эта цифра — 9, предыдущую цифру увеличиваем на единицу. Читают: «Тридцать две целых семьсот восемьдесят шесть тысячных приближенно равно тридцать две целых семьдесят девять сотых».

\ Округляя данное число до сотых, оставляем после запятой две цифры, а третью — отбрасываем. Так как отброшенная цифра — 1, предыдущую цифру оставляем без изменений. Читают: «Шесть целых девятьсот шестьдесят одна тысячная приближенно равно шесть целых девяносто шесть сотых».

\ При округлении до сотых оставляем после запятой две цифры, остальные — отбрасываем. Первая из отброшенных цифр — 3, поэтому предыдущую цифру не изменяем. Читают: «Семнадцать целых четыре тысячи тридцать девять десятитысячных приближенно равно семнадцать целых сорок восемь сотых».

\ Чтобы округлить данное число до сотых, после запятой оставим лишь две цифры, а остальные — отбросим. Первая из отброшенных цифр равна 5, поэтому предыдущую цифру увеличиваем на единицу. Читают: «Нуль целых тысяча двести пятьдесят четыре тысячных приближенно равно нуль целых тринадцать сотых».

\ При округлении числа до сотых оставляем после запятой две цифры, остальные — отбрасываем. Поскольку первая из отброшенных цифр — 7, предыдущую цифру увеличиваем на единицу. Читаем: «Пятьсот сорок девять целых, три тысячи семьдесят три десятитысячных приближенно равно пятьсот сорок девять целых, тридцать одна сотая».

Применения

Округление используется для того, чтобы работать с числами в пределах того количества знаков, которое соответствует реальной точности параметров вычислений (если эти значения представляют собой измеренные тем или иным образом реальные величины), реально достижимой точности вычислений либо желаемой точности результата. В прошлом округление промежуточных значений и результата имело прикладное значение (так как при расчётах на бумаге или с помощью примитивных устройств типа абака учёт лишних десятичных знаков может серьёзно увеличить объём работы). Сейчас оно остаётся элементом научной и инженерной культуры. В бухгалтерских приложениях, кроме того, использование округлений, в том числе промежуточных, может требоваться для защиты от вычислительных ошибок, связанных с конечной разрядностью вычислительных устройств.

32 Comments

Не правильная теория про если цифра 46.5 это не 47 а 46 это называется еще банковским округлением к ближайшему четному округляется если после запятой 5 и за ним нет никакой цифры

как округлить число 6,9?

Чтобы округлить число до целого, надо отбросить все числа, стоящие после запятой. Отбрасываем 9, поэтому предыдущее число следует увеличить на единицу. Значит, 6,9 приближенно равно семи целым.

На самом деле действительно не увеличивается цифра если после запятой 5 в любом финансовом учреждении

Гм. В таком случае финансовые учреждения в вопросах округления руководствуются не законами математики, а своими собственными соображениями.

Скажите, как округлить 46,466667. Запуталась

Если требуется округлить число до целого, то надо отбросить все цифры, стоящие после запятой. Первая из отброшенных цифр равна 4, поэтому предыдущую цифру не изменяем:

Уважаемая Светлана Ивановна. Плохо же Вы знакомы с правилами математики.

Правило. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т. е. последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная.

И Соответственно: Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиления не делаем, так как последняя сохраняемая цифра 6 — четная. Число 0,046 столь же близко к данному, как 0,047.

Уважаемый гость! Да будет Вам известно, в математике для округление числа существуют различные способы округления. В школе изучают один из них, состоящий в отбрасывании младших разрядов числа. Я рада за Вас, что Вы знаете другой способ, но неплохо бы не забывать и школьные знания.

Спасибо вам большое! Нужно было округлить 349,92. Получается 350. Спасибо за правило

как правильно округлить 5499,8?

Если речь об округлении до целого, то отбросить все цифры, стоящие после запятой. Отброшенная цифра — 8, следовательно, предыдущую увеличиваем на единицу. Значит, 5499,8 приближенно равно 5500 целым.

Доброго дня! А вот такой вопрос возник сейас: Есть три числа: 60.56% 11.73% и 27.71% Каким образом окрулить до целых знаечний? Чтобы в сумме то 100 осталось. Если просто округлять, то 61+12+28=101 Плучается неувязочка. (Если, как тыт писали, по «банковскому» методу — в данном случае получится, но в случае, например 60.5% и 39.5% получится опять что-то пало — 1% потеряем). Как быть?

О! помог метод от «гость 02.07.2015 12:11″ Благодарю»

Не знаю меня в школе учили так: 1.5 => 1 1.6 => 2 1.51 => 2 1.51 => 1.6

Возможно, Вас так учили.

По моему у Вас ошибочка в последнем выражении. 1.5 => 1 1.6 => 2 1.51 => 2 «1.51 => 1.5»

0, 855 до сотых помогите пожалуйста

0, 855≈0,86 (отброшена 5, предыдущую цифру увеличиваем на 1).

Округлить 2,465 до целого числа

2,465≈2 (первая отброшенная цифра — 4. Поэтому предыдущую оставляем без изменения).

Как округлить 2,4456 до целого?

2,4456 ≈ 2 (так как первая отброшенная цифра 4, предыдущую цифру оставляем без изменения).

Исходя из правил кругления: 1,45=1,5=2, следовательно 1,45=2. 1,(4)5 = 2. Так ли это?

Нет. Если требуется округлить 1,45 до целого, отбрасываем первую цифру после запятой. Поскольку это 4, предыдущую цифру не изменяем. Таким образом, 1,45≈1.

А если мне нужно округлить 103, это будет 100 или 105? (нужно округлить до 0 или 5)

Ирина, 103 — это уже целое число. Округлять до целого его не нужно. Если требуется округлить 103 до десятков, тогда 103≈100.

Источник

Функция ОКРУГЛ в Excel

Для обычного округления числа по математическим правилам существует функция ОКРУГЛ, которая имеет следующий синтаксис:

ОКРУГЛ(число или ссылка на округляемое число; количество оставляемых знаков).

число или ссылка на округляемое число – исходное число для округления;

количество оставляемых знаков – количество знаков после запятой.

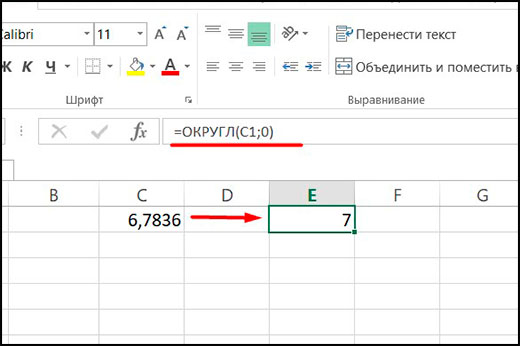
Например, формула округления в Excel до двух знаков после запятой выглядит так. 

Чтобы получить формулу округления в Excel до целого числа, во втором аргументе нужно поставить 0.

Встречаются и более сложные ситуации. Как, например, округлить до тысяч (три последние цифры являются нулями)? Многие поступают так. Делят число на 1 000, округляют до целого и затем снова умножают на 1 000. Это не лучший способ.

Функция ОКРУГЛ умеет округлять не только после запятой, но и до запятой, т.е. до тысяч, миллионов и т.д. Например, чтобы число 123456789 округлить до тысяч и получить 123457000, точность указывается с минусом.

На этом формулы округления в Эксель не заканчиваются.

Усечение десятичных чисел

Все методы, представленные ранее, выполняют JavaScript округление до десятых. Чтобы усечь положительное число до двух знаков после запятой, умножить его на 100, усечь снова, а затем полученный результат разделить на 100, нужно:

function truncated(num) {
    return Math.trunc(num * 100) / 100;
}
truncated(3.1416)
> 3.14

Если требуется что-то более гибкое, можно воспользоваться побитовым оператором:

function truncated(num, decimalPlaces) {    
    var numPowerConverter = Math.pow(10, decimalPlaces); 
    return ~~(num * numPowerConverter)/numPowerConverter;
}

Использование:

var randInt = 35.874993;
truncated(randInt,3);
> 35.874