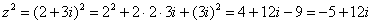Функции для работы с числами в 1с

Как округлить число настройкой формата ячейки?

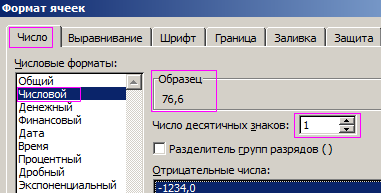
Давайте откроем таблицу, а потом переместим курсор в ячейку A1. Далее запишем туда дробное число 76,575. После этого делаем правый клик мышью, и далее выбираем опцию «Формат ячеек». Появится окошко. Его также можно вызвать с помощью нажатия клавиш Ctrl+1 или со вкладки «Главная» (инструмент «Число»).

В появившемся окне нас интересует числовой формат, в котором выбираем количество десятичных знаков, которое сейчас требуется. Представим, что они вообще сейчас мешают. Здесь можно в этом значении поставить 0.

1

После подтверждения нами внесенных изменений, у нас в ячейке появится итоговое значение – 77.

2

Все, как видим, достаточно нажать всего несколько кнопок мыши, и как по мановению волшебной палочки, начинает отображаться округленное число. Но нужно помнить, что применить его в математических вычислениях нельзя 

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Дополнительные функции

Excel содержит и более специфические формулы, использование которых необходимо только в исключительных случаях.

Например, функция ОТБР, которая отбрасывает числа от установленного разряда, то есть происходит не округление, а отсечение.

Функция ОКРВВЕРХ позволяет округлять значение ячейки до целого числа, при этом, если необходимо округлить в большую сторону кратно 100, необходимо указать точность 100, а если до 50, то, соответственно, 50.

Формула ОКРВНИЗ, аналогична предыдущей, только округляется вниз до целого. В зависимости от выбранной точности, можно округлить и до 5, однако это работает только для диапазона значений от 5,00 до 9,99.

Чтобы убрать округление, достаточно удалить из формулы любую из перечисленных функций, при этом исходное значения числа примет первоначальный вид.

Как видите, MS Excel обладает большим набором инструментов для работы с числами. Плюсом является то, что округление можно применять и к суммам, и к результатам вычисления выражений или функций. Описанные выше функции подойдут, как для бухгалтеров и людей, работающих с большими объемами чисел, так и для простых пользователей.

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

• Наименьшее натуральное число: единица (1).
• Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
• У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

1. Подчеркнуть цифру разряда, до которого надо округлить число.
2. Отделить все цифры справа от этого разряда вертикальной чертой.
3. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
4. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.

Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

Примеры:

• как округлить число 697 до десятков — 697 ≈ 700;
• как округлить число 980 до сотен — 980 ≈ 1000.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

• 7 882 000 = 7 882 тыс.
• 1 000 000 = 1 млн.

Усечение десятичных чисел

Все методы, представленные ранее, выполняют JavaScript округление до десятых. Чтобы усечь положительное число до двух знаков после запятой, умножить его на 100, усечь снова, а затем полученный результат разделить на 100, нужно:

function truncated(num) {
    return Math.trunc(num * 100) / 100;
}
truncated(3.1416)
> 3.14

Если требуется что-то более гибкое, можно воспользоваться побитовым оператором:

function truncated(num, decimalPlaces) {    
    var numPowerConverter = Math.pow(10, decimalPlaces); 
    return ~~(num * numPowerConverter)/numPowerConverter;
}

Использование:

var randInt = 35.874993;
truncated(randInt,3);
> 35.874

Для чего округлять числа?

JavaScript не хранит целые числа, поскольку их значения представлены в виде цифр с плавающей точкой. Многие дроби не могут быть представлены числом с определенным конечным количеством знаков после запятой, поэтому JavaScript может генерировать результаты, наподобие приведенного ниже:

0.1 * 0.2;
> 0.020000000000000004

На практике это не будет иметь никакого значения, поскольку речь идет о погрешности в 2 квинтилионные. Но это может отразиться на результате при работе с числами, которые представляют значения валют, процентов или размер файла. Поэтому нужно сделать JavaScript округление до целых или до определенного знака после запятой.

Округление чисел с плавающей запятой с помощью DoubleRounder

DoubleRounder — это утилита из библиотеки decimal4j. Она предоставляет быстрый метод округления double чисел до 18 знаков после запятой.

Последнюю версию библиотеки можно найти здесь. Чтобы подключить ее, добавьте зависимость в файл pom.xml:

<dependency>
    <groupId>org.decimal4j</groupId>
    <artifactId>decimal4j</artifactId>
    <version>1.0.3</version>
</dependency>

Пример использования утилиты:

DoubleRounder.round(PI, 3);

Но DoubleRounder дает сбой в нескольких сценариях. Например:

System.out.println(DoubleRounder.round(256.025d, 2));
// OUTPUTS: 256.02 вместо ожидаемого 256.03

JavaScript

JS Array
concat()
constructor
copyWithin()
entries()
every()
fill()
filter()
find()
findIndex()
forEach()
from()
includes()
indexOf()
isArray()
join()
keys()
length
lastIndexOf()
map()
pop()
prototype
push()
reduce()
reduceRight()
reverse()
shift()
slice()
some()
sort()
splice()
toString()
unshift()
valueOf()

JS Boolean
constructor
prototype
toString()
valueOf()

JS Classes
constructor()
extends
static
super

JS Date
constructor
getDate()
getDay()
getFullYear()
getHours()
getMilliseconds()
getMinutes()
getMonth()
getSeconds()
getTime()
getTimezoneOffset()
getUTCDate()
getUTCDay()
getUTCFullYear()
getUTCHours()
getUTCMilliseconds()
getUTCMinutes()
getUTCMonth()
getUTCSeconds()
now()
parse()
prototype
setDate()
setFullYear()
setHours()
setMilliseconds()
setMinutes()
setMonth()
setSeconds()
setTime()
setUTCDate()
setUTCFullYear()
setUTCHours()
setUTCMilliseconds()
setUTCMinutes()
setUTCMonth()
setUTCSeconds()
toDateString()
toISOString()
toJSON()
toLocaleDateString()
toLocaleTimeString()
toLocaleString()
toString()
toTimeString()
toUTCString()
UTC()
valueOf()

JS Error
name
message

JS Global
decodeURI()
decodeURIComponent()
encodeURI()
encodeURIComponent()
escape()
eval()
Infinity
isFinite()
isNaN()
NaN
Number()
parseFloat()
parseInt()
String()
undefined
unescape()

JS JSON
parse()
stringify()

JS Math
abs()
acos()
acosh()
asin()
asinh()
atan()
atan2()
atanh()
cbrt()
ceil()
clz32()
cos()
cosh()
E
exp()
expm1()
floor()
fround()
LN2
LN10
log()
log10()
log1p()
log2()
LOG2E
LOG10E
max()
min()
PI
pow()
random()
round()
sign()
sin()
sqrt()
SQRT1_2
SQRT2
tan()
tanh()
trunc()

JS Number
constructor
isFinite()
isInteger()
isNaN()
isSafeInteger()
MAX_VALUE
MIN_VALUE
NEGATIVE_INFINITY
NaN
POSITIVE_INFINITY
prototype
toExponential()
toFixed()
toLocaleString()
toPrecision()
toString()
valueOf()

JS OperatorsJS RegExp
constructor
compile()
exec()
g
global
i
ignoreCase
lastIndex
m
multiline
n+
n*
n?
n{X}
n{X,Y}
n{X,}
n$
^n
?=n
?!n
source
test()
toString()

(x|y)
.
\w
\W
\d
\D
\s
\S
\b
\B
\0
\n
\f
\r
\t
\v
\xxx
\xdd
\uxxxx

JS Statements
break
class
continue
debugger
do…while
for
for…in
for…of
function
if…else
return
switch
throw
try…catch
var
while

JS String
charAt()
charCodeAt()
concat()
constructor
endsWith()
fromCharCode()
includes()
indexOf()
lastIndexOf()
length
localeCompare()
match()
prototype
repeat()
replace()
search()
slice()
split()
startsWith()
substr()
substring()
toLocaleLowerCase()
toLocaleUpperCase()
toLowerCase()
toString()
toUpperCase()
trim()
valueOf()

Round() в Go 1.10

Для тех, кто не знаком с устройством float (я в их числе), этот код выглядит совершенно непонятно. Попробуем разобраться, что же он делает:

Похоже, что мы берём битовое представление числа, сдвигаем его и применяем маску. Согласно :

Рассматривая приведённые выше константы, мы видим, что сдвиг составляет 64 — 11 — 1, что означает 64 бита на число, 11 из которых используются для показателя степени, один — для знака и 52 оставшихся бита — для мантиссы. Это означает, что используемый сдвиг удаляет биты мантиссы, а маска удаляет бит знака, оставляя нас только с показателем степени.

В полученном числе показатель степени записан не как он есть, а с прибавлением числа 1023 (это делается для того чтобы записывать отрицательные показатели для очень маленьких чисел), что означает, что мы должны вычесть 1023 из e, вычисленного выше, чтобы получить фактический показатель. Иными словами, если e < bias, то мы имеем отрицательный показатель степени, что означает, что абсолютное значение float должно быть < 1. Действительно, дальше мы видим:

Здесь бит маскируется знаковым битом, это используется только для сохранения правильного знака: теперь мы можем полностью игнорировать мантиссу. Мы можем это сделать, потому что в этом случае нас интересует только показатель степени. Так как используется основание степени 2, а e < bias, мы знаем, что наименьший показатель, который может быть, равен -1, а 2 ^ -1 = 0,5. Кроме того, мантисса имеет некоторое значение 1.X. Таким образом, в зависимости от показателя наше число находится либо в диапазоне (0,5, 1), либо в диапазоне (0, 0,5). Поэтому во втором случае для правильного округления нам нужно добавить к числу единицу. Фух. Подробнее это описано в википедии.

Теперь разберём второй случай:

Наверное, вы думаете, что условие в этой ветке должно быть e > bias, чтобы покрыть все случаи с положительным показателем степени. Но вместо этого тут используется только их часть. Использование сдвига здесь особенно интересно, потому что кажется, что оно несравнимо с bias. Первое — это число битов смещения, а второе — численное смещение. Но, поскольку числа с плавающей точкой представлены как (1.мантисса) * 2 ^ X, то если X больше числа битов в мантиссе, мы гарантированно получим значение без дробной части. То есть показатель степени сместил десятичную точку вправо настолько, что мантисса окончательно пропала. Таким образом, выражение в этой ветке игнорирует числа с плавающей точкой, которые уже округлены.

Первая строка тут простая: вычитаем bias из e и получаем реальное значение показателя степени. Вторая строка добавляет к значению 0,5. Это работает, потому что старший бит мантиссы добавляет 0,5 к финальной сумме (см. представление в статье “Википедии” ниже). В этом случае эта сумма переполняет 52-битные границы мантиссы, показатель степени будет увеличен на 1. Значение показателя степени не сможет переполниться до знакового бита, так как оно не может быть больше bias+shift из примера выше. В любом случае, дробная часть очищается. Таким образом, если дробная часть была больше или равна 0,5, она будет увеличена на 1, в противном случае будет отброшена. Хитро и не очевидно до тех пор, пока мы не посмотрим глубже.

Почему Excel округляет большие числа?

Почти в любом калькуляторе или программе, если вводить слишком большие числа, они округляются до вида E+ и так далее. Excel не является исключением. Почему так происходит?Если число содержит больше 11 цифр, то он автоматически переводится в вид 1,111E+11. Такое представление числа называется экспоненциальным. Образовать такой способ представления вручную довольно сложно. Для этого необходимо вычислить логарифм числа и совершить еще несколько операций.

Если нам не нужно, чтобы Excel осуществлял округление огромных чисел, нам необходимо поставить перед соответствующим значением знак ‘. Предварительно нужно выставить текстовый формат. Но выполнять математические операции без использования специальных формул уже будет нельзя. 

Также допустим ввод значений в виде числа с пробелами. Excel автоматически превратит ячейку в текстовый формат. Реализовать же, чтобы программа электронных таблиц не делала этого, невозможно напрямую. Только через установку апострофа. 

Округление десятичных дробей

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,7
• 6,35
• 9,891

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

• разряд единиц;
• разряд десятков;
• разряд сотен;
• разряд тысяч.

Разряды дробной части:

• разряд десятых;
• разряд сотых;
• разряд тысячных.

Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248

При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То натуральное число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

• не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
• увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Как округлить до десятых. Оставить одну цифру после запятой. Изи!

Как округлить до сотых. Оставить две цифры после запятой.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Java: округление Double с помощью BigDecimal

Чтобы округлить тип double до n знаков после запятой, можно написать helper-метод:

private static double round(double value, int places) {
    if (places < 0) throw new IllegalArgumentException();
 
    BigDecimal bd = new BigDecimal(Double.toString(value));
    bd = bd.setScale(places, RoundingMode.HALF_UP);
    return bd.doubleValue();
}

Обратите внимание, что при создании экземпляра класса BigDecimal мы должны всегда использовать конструктор BigDecimal(String). Это позволяет избежать проблем с представлением неточных значений

Можно сделать то же самое, используя библиотеку Apache Commons Math:

<dependency>
    <groupId>org.apache.commons</groupId>
    <artifactId>commons-math3</artifactId>
    <version>3.5</version>
</dependency>

Актуальную версию этой библиотеки можно найти здесь. Для округления чисел применяется метод Precision.round() , который принимает два аргумента — значение и масштаб:

Precision.round(PI, 3);

По умолчанию он использует тот же метод округления HALF_UP, что хэлпер. Поэтому результаты должны быть одинаковыми.

Кроме этого можно изменить процесс приведения чисел, передав в качестве третьего параметра необходимый метод округления.

Целые

Отдельно мы рассмотрим округление до целых в Excel. Для проведения данной операции можно воспользоваться как уже рассмотренными командами, так и некоторыми другими.

• Формат. Для того чтобы ячейки автоматически округлялись до целочисленных значений, укажите в их формате значение — числовой, и количество знаков после запятой — 0.
• Все команды из предыдущего параграфа, применяющин параметр разрядности, могут использоваться как функция округления в Excel до целых. Для этого нужно указать разряд, равный нулю (0).
• ОКРВВЕРХ (значение; точность). Округляет число до большего значения. Точность определяет кратность результата. Например, ОКРВВЕРХ(12,753;1)=13. Но, ОКРВВЕРХ (12,753;2)=14. То есть число, кратное 2 (делящееся на 2 без остатка).
• ОКРВНИЗ (число; точность). Аналогично предыдущей команде только округляет до меньшего числа (ОКРВНИЗ(12,753;1)=12).
• ОТБР (число). Отбрасывает все знаки после запятой. Механика аналогична предыдущему случаю с точностью, равной 1.
• ОКРУГЛТ (число; точность). Формула округления в Excel, работающая по математическим правилам. Округляет до целых с определённой точностью, но самостоятельно определяет «вниз» или «вверх».
• ЧЁТН (значение). Работает так же, как и предыдущая функция при указании точности — 2, но округление производится исключительно «вверх».
• НЕЧЁТ (значение). Округляет до ближайшего большего нечетного числа. Пример: НЕЧЁТ (12,3231)=13, либо НЕЧЁТ (13,7345)=15.

Как округлить до целого числа

Как показано в предыдущем примере, достаточно просто убрать цифры в дробной части из формулы, как число сразу становится целым. Вот, как осуществляется округление! Но с помощью формулы можно получить настоящее целое число, а описанный выше способ – визуальный. Но логика не меняется в зависимости от того, реальный или визуальный результат будет отображаться. Все равно нужно выставлять ноль знаков.

Также возможно применение функций ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, чтобы оставлять только круглое число. Соответственно, первая округляет в сторону вверх, а вторая – в противоположном направлении по отношению к первой. В случае с отрицательными значениями – все наоборот, потому что округление осуществляется по модулю 

Round(Double, Int32, MidpointRounding)

Math.Round(d, decimals, mode) rounds a double-precision floating-point value to a specified number of fractional digits , and uses the specified rounding convention for midpoint values.

Syntax

The syntax of Round(d, decimals, mode) method is

Math.Round(Double d, Int32 decimals, MidpointRounding mode)

where

Parameter	Description
d	The double-precision floating-point number to be rounded.
decimals	The number of decimal places in the return value.
mode	Specification for how to round  if it is midway between two other numbers.

Return Value

The method returns rounded Double value.

Example 7 – Round(Double, Int32, MidpointRounding)

In this example, we will take some decimal double-precision floating-point numbers and round them to specific number of decimal points with different modes using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Double d, result;
        Int32 decimals;

        d = 10.2;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.AwayFromZero);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.AwayFromZero)       = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToEven);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToEven)             = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToNegativeInfinity);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToNegativeInfinity) = {result}");

        d = 10.2;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToPositiveInfinity);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToPositiveInfinity) = {result}");

        d = 10.8;
        decimals = 0;
        result = Math.Round(d, decimals, MidpointRounding.ToZero);
        Console.WriteLine($"Round({d}, {decimals}, MidpointRounding.ToZero)             = {result}");
    }
}

Output

Round(10.2, 0, MidpointRounding.AwayFromZero)       = 10
Round(10.8, 0, MidpointRounding.ToEven)             = 11
Round(10.8, 0, MidpointRounding.ToNegativeInfinity) = 10
Round(10.2, 0, MidpointRounding.ToPositiveInfinity) = 11
Round(10.8, 0, MidpointRounding.ToZero)             = 10

Округление вещественных чисел

Как мы уже разбирали, при присваивании переменной типа вещественного числа оно всегда округляется вниз до целого — его дробная часть просто отбрасывается.

А ведь легко можно представить ситуацию, когда дробное число нужно округлить просто до ближайшего целого или вообще вверх. Что делать в этой ситуации?

Для этого и для многих похожих случаев в Java есть класс , у которого есть методы , , .

Метод

Метод округляет число до ближайшего целого:

Но, как говорится, есть нюанс: результат работы этого метода — целочисленный тип (не ). Вещественные числа ведь могут быть очень большими, поэтому разработчики Java решили использовать самый большой целочисленный тип, который есть в Java — .

Поэтому чтобы присвоить результат в переменную типа , программист должен явно указать компилятору, что он согласен с возможной потерей данных (вдруг число не поместится в тип ).

Примеры:

Команда	Результат

Метод

Метод округляет число до целого вверх, примеры:

Команда	Результат

Метод

Метод округляет число до целого вниз, примеры:

Команда	Результат

Хотя, для округления числа до целого вниз, будет проще использовать просто оператор приведения типа — :

Команда	Результат

Если вам сложно запомнить эти команды, вам поможет небольшой урок английского:

• — математика
• — круг/округлять
• — потолок
• — пол

Округление в Excel в большую сторону при помощи функции ОКРУГЛВВЕРХ

Пользователь может самостоятельно задавать направление для округления. С помощью функции ОКРУГЛВВЕРХ можно убрать лишни цифры или осуществить округление целого числа до того, которое оказывается выше.

Пример использования этой формулы можно увидеть на этом скриншоте.

6

Основное отличие этой функции от ОКРУГЛ заключается в том, что всегда функция обеспечивает округление с избытком. Если имеются какие-либо разряды числа, округление осуществляется до определенного их количества.

Синтаксис функции ОКРУГЛВВЕРХ

В состав этой функции ходит два аргумента. В целом, функция выглядит следующим образом.

=ОКРУГЛВВЕРХ(76,9;0)

А теперь давайте более подробно разберемся, какие у нее аргументы.

Аргументы функции ОКРУГЛВВЕРХ

Синтаксис у этой функции, как видим, очень простой. Аргументы следующие:1. Число. Это какое-угодно число, для которого требуется округление.

1. Число разрядов. Здесь записывается количество разрядов, которое должно остаться после того, как округление будет осуществлено.

Таким образом, по синтаксису эта формула ничем не отличается от ОКРУГЛ. От модальности числа зависит то, какие именно числа будут сокращаться. Если второй аргумент положительный, то округление оуществляется в правой части от запятой. Если же он отрицательный – то с левой.