Функция предсказ в excel

Линия тренда в Excel

Приложение Эксель предоставляет возможность построение линии тренда при помощи графика. При этом, исходные данные для его формирования берутся из заранее подготовленной таблицы.

Построение графика

Для того, чтобы построить график, нужно иметь готовую таблицу, на основании которой он будет формироваться. В качестве примера возьмем данные о стоимости доллара в рублях за определенный период времени.

1. Строим таблицу, где в одном столбике будут располагаться временные отрезки (в нашем случае даты), а в другом – величина, динамика которой будет отображаться в графике.

Выделяем данную таблицу. Переходим во вкладку «Вставка». Там на ленте в блоке инструментов «Диаграммы» кликаем по кнопке «График». Из представленного списка выбираем самый первый вариант.

После этого график будет построен, но его нужно ещё доработать. Делаем заголовок графика. Для этого кликаем по нему. В появившейся группе вкладок «Работа с диаграммами» переходим во вкладку «Макет». В ней кликаем по кнопке «Название диаграммы». В открывшемся списке выбираем пункт «Над диаграммой».

Затем подписываем оси. В той же вкладке «Макет» кликаем по кнопке на ленте «Названия осей». Последовательно переходим по пунктам «Название основной горизонтальной оси» и «Название под осью».

В появившемся поле вписываем название горизонтальной оси, согласно контексту расположенных на ней данных.

Для того, чтобы присвоить наименование вертикальной оси также используем вкладку «Макет». Кликаем по кнопке «Название осей». Последовательно перемещаемся по пунктам всплывающего меню «Название основной вертикальной оси» и «Повернутое название». Именно такой тип расположения наименования оси будет наиболее удобен для нашего вида диаграмм.

Создание линии тренда

Теперь нужно непосредственно добавить линию тренда.

1. Находясь во вкладке «Макет» кликаем по кнопке «Линия тренда», которая расположена в блоке инструментов «Анализ». Из открывшегося списка выбираем пункт «Экспоненциальное приближение» или «Линейное приближение».

После этого, линия тренда добавляется на график. По умолчанию она имеет черный цвет.

Настройка линии тренда

Имеется возможность дополнительной настройки линии.

1. Последовательно переходим во вкладке «Макет» по пунктам меню «Анализ», «Линия тренда» и «Дополнительные параметры линии тренда…».

Открывается окно параметров, можно произвести различные настройки. Например, можно выполнить изменение типа сглаживания и аппроксимации, выбрав один из шести пунктов:

• Полиномиальная;
• Линейная;
• Степенная;
• Логарифмическая;
• Экспоненциальная;
• Линейная фильтрация.

Для того, чтобы определить достоверность нашей модели, устанавливаем галочку около пункта «Поместить на диаграмму величину достоверности аппроксимации». Чтобы посмотреть результат, жмем на кнопку «Закрыть».

Если данный показатель равен 1, то модель максимально достоверна. Чем дальше уровень от единицы, тем меньше достоверность.

Если вас не удовлетворяет уровень достоверности, то можете вернуться опять в параметры и сменить тип сглаживания и аппроксимации. Затем, сформировать коэффициент заново.

Прогнозирование

Главной задачей линии тренда является возможность составить по ней прогноз дальнейшего развития событий.

1. Опять переходим в параметры. В блоке настроек «Прогноз» в соответствующих полях указываем насколько периодов вперед или назад нужно продолжить линию тренда для прогнозирования. Жмем на кнопку «Закрыть».

Опять переходим к графику. В нем видно, что линия удлинена. Теперь по ней можно определить, какой приблизительный показатель прогнозируется на определенную дату при сохранении текущей тенденции.

Как видим, в Эксель не составляет труда построить линию тренда. Программа предоставляет инструменты, чтобы её можно было настроить для максимально корректного отображения показателей. На основании графика можно сделать прогноз на конкретный временной период.

Реализация функции MS Excel «ПРЕДСКАЗ»

У кого-нибудь имеется готовая реализация функции на С#? Знаю как использовать функцию в своей программе через Microsoft.Office.Interop.Excel и WorksheetFunction. Но, хотелось бы, целиком на C#. Сам еще написать не пробовал, формулы не сложные вроде, но, вдруг у кого готовое решение завалялось.

Экспорт в Excel: Прекращена работа программы «Microsoft Excel»Файл сохраняется успешно, но поле строки excelApp.Quit(); Появляется окно ошибки Excel: .

Ошибка CS0019: Оператор «*» не может применяться к операндам типа «decimal» и «float»Здравствуйте! Писал приложение и наткнулся на интересную ошибку (честно говоря, я не совсем понимаю.

Переопределить операции «+» «=» «-» для экземпляров моего классаДобрый день. Мне нужно переопределить операции «+» «=» «-» для экземпляров моего класса. Я вижу это.

Как рассчитать коэффициент корреляции в Excel

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

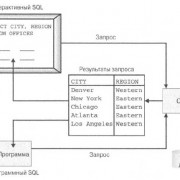
Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

Параметры Parameters

Имя Name	Обязательный или необязательный Required/Optional	Тип данных Data type	Описание Description
Arg1 Arg1	Обязательный Required	Double Double	x — точка данных, для которой требуется предсказать значение. x – the data point for which you want to predict a value.
Arg2 Arg2	Обязательный Required	Variant Variant	известные_значения_y — зависимый массив или диапазон данных. known_y’s – the dependent array or range of data.
Arg3 Arg3	Обязательный Required	Variant Variant	Известные_значения_x — независимый массив или диапазон данных. known_x’s – the independent array or range of data.

Инструкция

1. Один из самых простых способов – внести текущую информацию в массив и тем самым однозначно выстроить схему функционирования тренда. Чтобы совершить предполагаемое действие, на странице выстроенных данных обозначьте две, три или более ячеек для диапазона будущей схемы и непременно скопируйте диаграмму. Существуют несколько видов диаграмм, которые поддерживают такую функцию, например гистограмма, точечная и некоторые другие виды.
2. В разделе с диаграммой найдите графу с добавлением линии тренда. Опция «Добавить линию тренда»

В появившейся вкладке необходимо выбрать соответствующий вид линии тренда или по-другому аппроксимацию данных.

Вкладка «Линия тренда»

Вся введенная информация будет считываться произвольно, поскольку никаких сложных алгоритмов проведено не было.

Вам нужно просто определить вид функции наиболее подходящий для графика введенных данных, например, линейный, экспоненциальный, логарифмический или какой-либо другой. Можно выстроить две или три линии, если есть сомнения при решении вида аппроксимации, или же обратиться к пункту «параметры» и обозначить место (в дальнейшем именуемая как R^2), отметив данные в качестве диаграммы достоверности аппроксимации.
Для построения наиболее точного прогноза, сравните несколько значений в формате R^2, расположенных на разных линиях, и тогда вы найдете самые достоверные сведения вашего графика. Выбор типа линии будет зависеть от того, насколько итог измерения R^2 будет равняться единице. В той же графе с параметрами нужно обязательно указать время проведения прогнозирования.
Данный метод построения тренда будет относительно точным, следовательно, на всякий случай, произведите самую простейшую обработку статических данных. Это в разы облегчит работу построения прогноза.
На случай, когда действующие данные описаны при помощи линейного уравнения, достаточно будет отметить их и произвести автоматическое заполнение на необходимую сумму периодов, так же сумму ячеек. При этом совершенно не нужно искать сумму равенства R^2, поскольку прогнозирование было преждевременно составлено уравнением в простейшем варианте.
Однако, если возникло предположение, что полученные данные могут быть составлены благодаря экспоненциальному уравнению, обозначьте изначальный интервал и проведите автоматическое заполнение нужного количества ячеек. Главное знать, что автоматическое заполнение не поможет выстроить иные разновидности линий, помимо двух описанных выше.
Чтобы произвести наиболее точное прогнозирование, понадобится использовать хотя бы одну статическую функцию (например, «тенденцию», «предсказание», «рост» и так далее). При этом все исчисления прогнозов необходимо будет совершать самостоятельно. Но, если есть нужда провести комплексную и составную аналитику данных, функция «пакет анализа» найдет свое применение. Однако, данная подстройка не состоит в стандартном пакете Microsoft Office.

Функция ПРЕДСКАЗ

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки

Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы

Для удобства также приводим ссылку на оригинал (на английском языке).

В этой статье описаны синтаксис формулы и использование функции ПРЕДСКАЗ в Microsoft Excel.

Примечание: В Excel 2016 эта функция была заменена прогнозом . ЛИНЕЙная , как часть новых функций прогнозирования. Она по-прежнему доступна для обеспечения обратной совместимости, но рекомендуется использовать функцию Новая функция в Excel 2016.

Вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для прогнозирования будущих продаж, потребностей в оборудовании или тенденций потребления.

Аргументы функции ПРЕДСКАЗ описаны ниже.

x — обязательный аргумент. Точка данных, для которой предсказывается значение.

Известные_значения_y — обязательный аргумент. Зависимый массив или интервал данных.

Известные_значения_x — обязательный аргумент. Независимый массив или интервал данных.

Если x не является числом, функция ПРЕДСКАЗ возвращает #VALUE! значение ошибки #ЗНАЧ!.

Если аргументы «известные_значения_y» и «известные_значения_x» пусты или количество точек данных в этих аргументах не совпадает, функция ПРЕДСКАЗ возвращает значение ошибки #Н/Д.

Если значение аргумента «известные_значения_x» равно нулю, функция ПРЕДСКАЗ возвращает #DIV/0! значение ошибки #ЗНАЧ!.

Уравнение для функции ПРЕДСКАЗ имеет вид a+bx, где:

где x и y — средние значения выборок СРЗНАЧ(известные_значения_x) и СРЗНАЧ(известные_значения_y).

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Функция РОСТ()

Функция РОСТ() рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных. Функция РОСТ возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений. Функция рабочего листа РОСТ может применяться также для аппроксимации существующих x- и y-значений экспоненциальной кривой.

РОСТ (известные_значения_y;известные_значения_x;новые_значения_x; конст)

Известные_значения_y — множество значений y, которые уже известны в уравнении

Если массив «известные_значения_y» содержит один столбец, каждый столбец массива «известные_значения_x» интерпретируется как отдельная переменная.

Если массив «известные_значения_y» содержит одну строку, каждая строка массива «известные_значения_x» интерпретируется как отдельная переменная.

Если какие-либо числа в массиве «известные_значения_y» равны 0 или имеют отрицательное значение, функция РОСТ возвращает значение ошибки #ЧИСЛО!. Известные_значения_x — необязательное множество значений x, которые уже известны в уравнении

Массив «известные_значения_x» может содержать одно или несколько множеств переменных. Если используется только одна переменная, множества «известные_значения_y» и «известные_значения_x» могут иметь любую длину, но их размерности должны совпадать. Если используется более одной переменной, аргумент «известные_значения_y» должен быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).

Если аргумент «известные_значения_x» опущен, то предполагается, что это массив того же размера, что и «известные_значения_y».

Новые_значения_x — новые значения x, для которых РОСТ возвращает соответствующие значения y.

Аргумент «новые_значения_x» должен содержать столбец (или строку) для каждой независимой переменной, так же как и «известные_значения_x». Таким образом, если массив «известные_значения_y» состоит из одного столбца, то столько же столбцов должны иметь массивы «известные_значения_x» и «новые_значения_x». Если массив «известные_значения_y» состоит из одной строки, столько же строк должно содержаться в массивах «известные_значения_x» и «новые_значения_x».

Если аргумент «новые_значения_x» опущен, предполагается, что он совпадает с аргументом «известные_значения_x».

Если опущены оба аргумента «известные_значения_x» и «новые_значения_x», то предполагается, что каждый из них представляет собой массив того же размера, что и «известные_значения_y».

Конст — логическое значение, которое указывает, должна ли константа b равняться 1. Если аргумент «конст» имеет значение ИСТИНА или опущен, b вычисляется обычным образом. Если аргумент «конст» имеет значение ЛОЖЬ, то предполагается, что b = 1, а значения m подбираются таким образом, чтобы выполнялось равенство y = m^x.

Замечания Формулы, возвращающие массивы, должны быть введены как формулы массивов после того, как будет выделено соответствующее количество ячеек. При вводе константы массива для аргумента (например, «известные_значения_x») следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.

Мультипликативное экспоненциальное сглаживание Холта-Винтерса

Метод называется мультипликативным (от multiplicate — умножать), поскольку использует умножение для учета сезонности:

Спрос в момент t = (уровень + t × тренд) × сезонная поправка для момента t × все оставшиеся нерегулярные поправки, которые мы не можем учесть

Сглаживание Холта-Винтерса также называют тройным экспоненциальным сглаживанием, потому что у него три сглаживающих параметра (альфа, гамма и сезонный фактор – дельта). Например, если имеется 12-месячный сезонный цикл:

Прогноз на месяц 39 = (уровень₃₆ + 3 × тренд₃₆) х сезонность₂₇

Анализируя данные, необходимо выяснить, что в серии данных является трендом, а что — сезонностью. Чтобы выполнить вычисления по методу Холта-Винтерса, необходимо:

• Сгладить исторические данные методом скользящего среднего.
• Сравнить сглаженную версию временного ряда данных с оригиналом, чтобы получить приблизительную оценку сезонности.
• Получить новые данные без сезонного компонента.
• Найти приближения уровня и тренда на основе этих новых данных.

Начните с исходных данных (столбцы А и В на рис. 12) и добавьте столбец С со сглаженными значениями на основе скользящего среднего. Так как сезонность имеет 12-месячные циклы, имеет смысл использовать среднее за 12 месяцев. С этим средним есть небольшая проблема. 12 – четное число. Если вы сглаживаете спрос за месяц 7, стоит ли считать его средним спросом с 1-го по 12-й месяц или со 2-го по 13-й? Чтобы справиться с этим затруднением, нужно сгладить спрос с помощью «скользящего среднего 2×12». Т.е., взять половину от двух средних с 1 по 12-й месяц и со 2 по 13. Формула в ячейке С8: =(СРЗНАЧ(B3:B14)+СРЗНАЧ(B2:B13))/2.

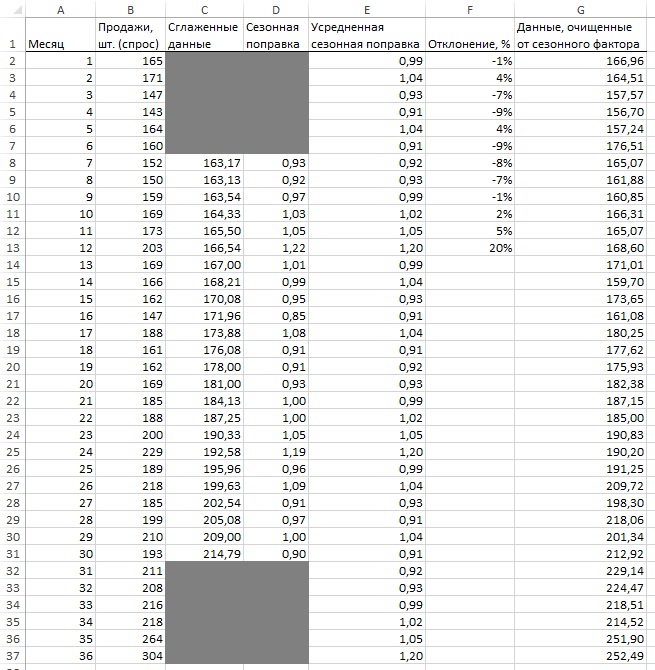
Рис. 12. Данные, очищенные от сезонного фактора

Сглаженные данных для месяцев 1–6 и 31–36 получить нельзя, так как не хватает предыдущих и последующих периодов. Для наглядности исходные и сглаженные данные можно отразить на диаграмме (рис. 13).

Рис. 13. Сглаженные данные спроса

Теперь в столбце D разделите оригинальную величину на сглаженную и получите приблизительное значение сезонной поправки (столбец D на рис. 12). Формула в ячейке D8: =B8/C8

Обратите внимание на всплески в 20% выше нормального спроса в месяцах 12 и 24 (декабрь), в то время как весной наблюдаются провалы. Эта техника сглаживания дала вам две точечные оценки для каждого месяца (всего 24 месяца)

В столбце Е найдено среднее значение этих двух факторов. Формула в ячейке Е1: =СРЗНАЧ(D14;D26). Для наглядности уровень сезонных колебаний можно представить графически (рис. 14).

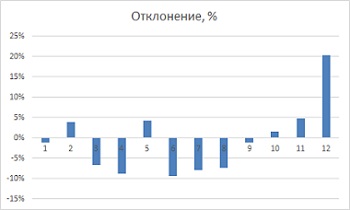
Рис. 14. Сезонные колебания

Теперь можно получить данные, скорректированные на сезонные колебания. Формула в ячейке G1: =B2/E2. Постройте график на основе данных столбца G, дополните его линией тренда, выведите уравнение тренда на диаграмму (рис. 15), и используйте коэффициенты в последующих расчетах.

Рис. 15. Данные, скорректированные на сезонные колебания

Сформируйте новый лист, как показано на рис. 16. Значения в диапазон Е5:Е16 подставьте с рис. 12 области Е2:Е13. Значения С16 и D16 возьмите из уравнения линии тренда на рис. 15. Значения констант сглаживания установите для начала на отметке 0,5. Растяните значения в строке 17 на диапазон месяцев с 1 по 36. Запустите Поиск решения для оптимизации коэффициентов сглаживания (рис. 18). Формула в ячейке В53: =(C$52+(A53-A$52)*D$52)*E41.

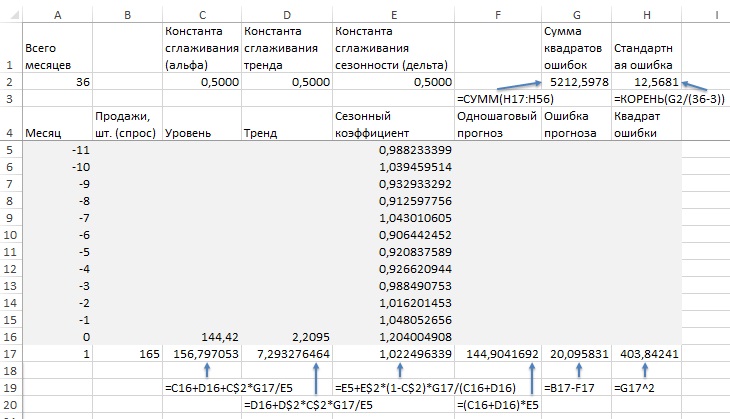
Рис. 16. Данные для прогноза Холта-Винтера

Рис. 17. График прогноза Холта-Винтерса

Теперь в сделанном прогнозе нужно проверить автокорреляции (рис. 18). Так как все значения расположились между верхней и нижней границами, вы понимаете, что модель неплохо поработала над пониманием структуры значений спроса.

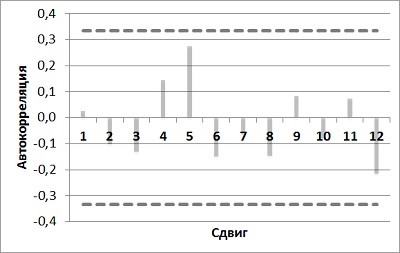
Рис. 18. Коррелограмма модели Холта-Винтерса

Алгоритм прогнозирования объёма продаж в MS Excel

На сегодняшний день наука достаточно далеко продвинулась в разработке технологий прогнозирования. Специалистам хорошо известны методы нейросетевого прогнозирования, нечёткой логики и т.п. Разработаны соответствующие программные пакеты, но на практике они, к сожалению, не всегда доступны рядовому пользователю, а в то же время многие из этих проблем можно достаточно успешно решать, используя методы исследования операций, в частности имитационное моделирование, теорию игр, регрессионный и трендовый анализ, реализуя эти алгоритмы в широко известном и распространённом пакете прикладных программ MS Excel.

В данной статье представлен один из возможных алгоритмов построения прогноза объёма реализации для продуктов с сезонным характером продаж. Сразу следует отметить, что перечень таких товаров гораздо шире, чем это кажется. Дело в том, что понятие “сезон” в прогнозировании применим к любым систематическим колебаниям, например, если речь идёт об изучении товарооборота в течение недели под термином “сезон” понимается один день. Кроме того, цикл колебаний может существенно отличаться (как в большую, так и в меньшую сторону) от величины один год. И если удаётся выявить величину цикла этих колебаний, то такой временной ряд можно использовать для прогнозирования с использованием аддитивных и мультипликативных моделей.

Аддитивную модель прогнозирования можно представить в виде формулы:

где: F – прогнозируемое значение; Т – тренд; S – сезонная компонента; Е – ошибка прогноза.

Применение мультипликативных моделей обусловлено тем, что в некоторых временных рядах значение сезонной компоненты представляет собой определенную долю трендового значения. Эти модели можно представить формулой:

На практике отличить аддитивную модель от мультипликативной можно по величине сезонной вариации. Аддитивной модели присуща практически постоянная сезонная вариация, тогда как у мультипликативной она возрастает или убывает, графически это выражается в изменении амплитуды колебания сезонного фактора, как это показано на рисунке 1.

Рис. 1. Аддитивная и мультипликативные модели прогнозирования.

Алгоритм построения прогнозной модели

Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели:

1.Определяется тренд, наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.

2.Вычитая из фактических значений объёмов продаж значения тренда, определяют величины сезонной компоненты и корректируют таким образом, чтобы их сумма была равна нулю.

3.Рассчитываются ошибки модели как разности между фактическими значениями и значениями модели.

4.Строится модель прогнозирования:

где: F– прогнозируемое значение; Т– тренд; S – сезонная компонента; Е — ошибка модели.

5.На основе модели строится окончательный прогноз объёма продаж. Для этого предлагается использовать методы экспоненциального сглаживания, что позволяет учесть возможное будущее изменение экономических тенденций, на основе которых построена трендовая модель. Сущность данной поправки заключается в том, что она нивелирует недостаток адаптивных моделей, а именно, позволяет быстро учесть наметившиеся новые экономические тенденции.

где: F_{пр t} — прогнозное значение объёма продаж; F_{ф t-}1 – фактическое значение объёма продаж в предыдущем году; F_{м t} — значение модели; а – константа сглаживания

Практическая реализация данного метода выявила следующие его особенности:

• для составления прогноза необходимо точно знать величину сезона. Исследования показывают, что множество продуктов имеют сезонный характер, величина сезона при этом может быть различной и колебаться от одной недели до десяти лет и более;
• применение полиномиального тренда вместо линейного позволяет значительно сократить ошибку модели;
• при наличии достаточного количества данных метод даёт хорошую аппроксимацию и может быть эффективно использован при прогнозировании объема продаж в инвестиционном проектировании.

Применение алгоритма рассмотрим на следующем примере.

Исходные данные: объёмы реализации продукции за два сезона. В качестве исходной информации для прогнозирования была использована информация об объёмах сбыта мороженого “Пломбир” одной из фирм в Нижнем Новгороде. Данная статистика характеризуется тем, что значения объёма продаж имеют выраженный сезонный характер с возрастающим трендом. Исходная информация представлена в табл. 1.

Таблица 1. Фактические объёмы реализации продукции

Прогноз прибыли за месяц с использованием функции РОСТ в Excel

Пример 3. Экономист развивающегося предприятия ведет учет прибыли, при этом в таблице содержатся три вектора данных: месяц, число сделок, общая сумма прибыли. Необходимо спрогнозировать прибыль на следующий месяц при двух условиях:

• Количество сделок будет равно показателю за предыдущий месяц;
• Количество сделок увеличится на 2.

Вводим функцию РОСТ и получаем ошибку #ЗНАЧ!:

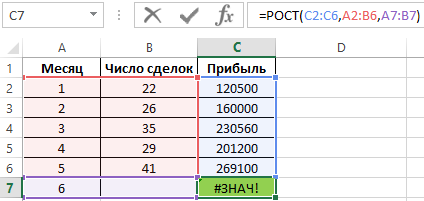
Внимание! В данном случае для прогнозирования прибыли будет использовано сочетание двух факторов: номер месяца и число сделок. Поэтому в качестве аргумента необходимо передать диапазон значений A2:B6, а в качестве аргумента – диапазон A7:B7

Для определения прибыли при условии, что число сделок составит 41, запишем следующую формулу:

Теперь увеличим количество сделок на 2-е:

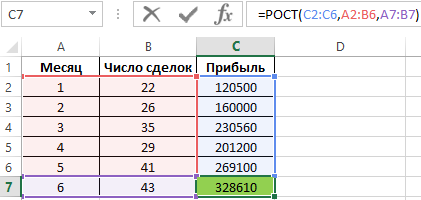
Как и ожидалось, прогнозируемая прибыль увеличилась. Пример наглядно демонстрирует, что для увеличения точности предсказания можно использовать 2 и более зависящих друг от друга параметров.

Из чего состоит временной ряд

Уровни временного ряда (Yt) представляют из себя сумму двух компонент:

1. Регулярную составляющую
2. Случайную составляющую

В свою очередь регулярная составляющая состоит из:

1. Тренда
2. Сезонности
3. Циклической составляющей

Однако, в модели необязательно наличие всех этих компонент сразу.

Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.

То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:

1. Тренд (Tt)
2. Сезонность (St)
3. Цикличность (Ct)
4. Случайные возмущения (Et)

Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.

Шаг 5

Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

yi — спрогнозированные уровни ряда,

yi* — фактические уровни ряда,

n — количество складываемых элементов.

Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.

Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.

Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении

Полезные ссылки:

• Ссылка на пример Google Sheets
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
• Бывшев В.А. Эконометрика

Екатерина Шипова

Магистр прикладной математики и информатики, веб-аналитик. Сертифицированный специалист Google Аnalytics и Яндекс.Метрика.

• Прогнозирование продаж в Excel с учетом сезонности — 27.06.2018
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности — 05.06.2018
• Когортный анализ. Сколько пользователей к вам вернулось? — 24.05.2018

Заключение

Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.

Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.

Файл с расчетамиСкачать

 

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.