Pythonista. привет, python

Содержание:

Числа: целые, вещественные, комплексные
- Целые числа (int)
- Вещественные числа (float)
  - Дополнительные методы
Округление десятичного числа
Специальные константы
- Pie
- Число Эйлера
Математические операторы Python 3
Исключения и трассировка.
Комплексные числа (complex)
Вещественные числа (float)
Умножение и деление
Операции со строками
- 3. Объединение с преобразованием
- 4. Поиск подстроки
- 5. Получение подстроки
- 7. Очистка строк
- 9. Конвертирование строк
- 10. Длина строк
- 11. Перебор строки
Кавычки
Целые числа и числа с плавающей запятой
- Целые числа
- Числа с плавающей запятой
7.5. Дискретное преобразование Фурье
Список
Операторы присваивания
История
Операторы присваивания
Дополнение 1: Как вызывать магические методы
История
Как посчитать сумму введенных чисел?
Как посчитать сумму введенных чисел?
7.3. Статистика
Модуль random
- Задание 4.3 Камень, ножницы, бумага
Квадратный корень — что это?
Математические операторы Python 3
Библиотека math

Числа: целые, вещественные, комплексные

Числа в Python 3: целые, вещественные, комплексные. Работа с числами и операции над ними.

Целые числа (int)

Числа в Python 3 ничем не отличаются от обычных чисел. Они поддерживают набор самых обычных математических операций:

x + y	Сложение
x — y	Вычитание
x * y	Умножение
x / y	Деление
x // y	Получение целой части от деления
x % y	Остаток от деления
-x	Смена знака числа
abs(x)	Модуль числа
divmod(x, y)	Пара (x // y, x % y)
x ** y	Возведение в степень
pow(x, y)	x y по модулю (если модуль задан)

Также нужно отметить, что целые числа в python 3, в отличие от многих других языков, поддерживают длинную арифметику (однако, это требует больше памяти).

Битовые операции

Над целыми числами также можно производить битовые операции

x \| y	Побитовое или
x ^ y	Побитовое исключающее или
x & y	Побитовое и
x > y	Битовый сдвиг вправо

Инверсия битов

Дополнительные методы

int.bit_length() — количество бит, необходимых для представления числа в двоичном виде, без учёта знака и лидирующих нулей.

int.to_bytes(length, byteorder, *, signed=False) — возвращает строку байтов, представляющих это число.

classmethod int.from_bytes(bytes, byteorder, *, signed=False) — возвращает число из данной строки байтов.

Системы счисления

Те, у кого в школе была информатика, знают, что числа могут быть представлены не только в десятичной системе счисления. К примеру, в компьютере используется двоичный код, и, к примеру, число 19 в двоичной системе счисления будет выглядеть как 10011. Также иногда нужно переводить числа из одной системы счисления в другую. Python для этого предоставляет несколько функций:

int(, ) — преобразование к целому числу в десятичной системе счисления. По умолчанию система счисления десятичная, но можно задать любое основание от 2 до 36 включительно.
bin(x) — преобразование целого числа в двоичную строку.
hex(х) — преобразование целого числа в шестнадцатеричную строку.
oct(х) — преобразование целого числа в восьмеричную строку.

Вещественные числа (float)

Вещественные числа поддерживают те же операции, что и целые. Однако (из-за представления чисел в компьютере) вещественные числа неточны, и это может привести к ошибкам:

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

Простенькие примеры работы с числами:

Дополнительные методы

float.as_integer_ratio() — пара целых чисел, чьё отношение равно этому числу.

float.is_integer() — является ли значение целым числом.

float.hex() — переводит float в hex (шестнадцатеричную систему счисления).

classmethod float.fromhex(s) — float из шестнадцатеричной строки.

Помимо стандартных выражений для работы с числами (а в Python их не так уж и много), в составе Python есть несколько полезных модулей.

Модуль math предоставляет более сложные математические функции.

Модуль random реализует генератор случайных чисел и функции случайного выбора.

Также для работы с комплексными числами используется также модуль cmath.

Округление десятичного числа

Осваиваем python: математические операции

При работе с десятичными числами важно иметь возможность быстро округлить его до N знаков после запятой. Строенная функция round() выполняет эту задачу

При этом ей необходимо два числа: A – число, которое нужно округлить, B – количество знаков после запятой.

Например:

Попробуйте написать простую программу, которая будет подсчитывать чаевые. К примеру, три человека хотят разделить счет в ресторане в $87.93 и оставить 20% чаевых.

В результате получилось число с большим количеством десятичных знаков. Функция round() округлила его до двух знаков после запятой.

Чтобы округлить десятичное число до целого числа, задайте 0 в качестве второго параметра (в данном случае тип данных не преобразуется, после запятой будет 0):

Функция round() может работать и с целыми числами. Если в качестве первого параметра задано целое число, в результате функция также вернёт целое число.

Специальные константы

Python if…else statement

Математическая библиотека в Python содержит две важные константы.

Pie

Первая – это Pie (π), очень популярная математическая константа. Он обозначает отношение длины окружности к диаметру круга и имеет значение 3,141592653589793. Чтобы получить к нему доступ, мы сначала импортируем математическую библиотеку следующим образом:

import math

Затем мы можем получить доступ к этой константе с помощью pi:

math.pi

Вывод:

3.141592653589793

Вы можете использовать эту константу для вычисления площади или длины окружности. Следующий пример демонстрирует это:

import math

radius = 2
print('The area of a circle with a radius of 2 is:', math.pi * (radius ** 2))

Вывод:

The area of a circle with a radius of 2 is: 12.566370614359172

Мы увеличили значение радиуса до степени 2, а затем умножили его на круговую диаграмму в соответствии с формулой площади πr 2 .

Число Эйлера

Число Эйлера (e), являющееся основанием натурального логарифма, также определено в библиотеке Math. Мы можем получить к нему доступ следующим образом:

math.e

Вывод:

2.718281828459045

В следующем примере показано, как использовать указанную выше константу:

import math

print((math.e + 6 / 2) * 4.32)

Вывод:

24.702977498943074

Математические операторы Python 3

Операторы python

Оператор – это символ, которая обозначает операцию. Например, в математике знак плюса или + – это оператор сложения.

Мы рассмотрим схожие операторы, которые перешли в Python из математики. Но другие операторы специфичны именно для программирования.

Ниже представлена таблица с кратким обзором математических операторов, доступных в Python.

Операция	Возвращаемое значение
x + y	Сумма x и y.
x — y	Разность x и y.
-x	Изменение знака x.
+x	Тождественность x.
x * y	Произведение x и y.
x / y	Частное от деления x на y.
x // y	Частное от целочисленного деления x на y.
x % y	Остаток от деления x / y.
x ** y	x в степени y.

Исключения и трассировка.

В Python также как и в алгебре деление на 0 запрещено. При попытке выполнения такой операции происходит исключение. Сообщая об исключение, Python выдает трассировку стека. В трассировке указано, что произошло исключение типа ZeroDivisionError, большая часть исключений заканчивается суффиксом Error. Ошибка division by zero — деление на ноль.

>>> 5 / 0Traceback (most recent call last):
File «<stdin>», line 1, in <module>
ZeroDivisionError: division by zero

1. Установка Python 2. Выбор текстового редактора 3. Запуск программ Python в командной строке 4. Числа и арифметические операторы Python 5.Строки и функция Print в Python 6. Списки и кортежи в Python 7. Сегментация последовательностей в Python 8. Цикл for и функция range в Python 9. Команда if и функция input в Python 10. Словари в Python 11. Множества в Python 12. Цикл while в Python 13. Функции в Python 14. Классы в Python 15. Файлы и исключения в Python 16. Функции json. Сохранение данных Python 17.Тестирование функций и классов на Python>>> 5 -?

Please enable JavaScript to view the comments powered by Disqus.

Комплексные числа (complex)

В Python встроены также и комплексные числа:

>>> x = complex(1, 2)
>>> print(x)
(1+2j)
>>> y = complex(3, 4)
>>> print(y)
(3+4j)
>>> z = x + y
>>> print(x)
(1+2j)
>>> print(z)
(4+6j)
>>> z = x * y
>>> print(z)
(-5+10j)
>>> z = x  y
>>> print(z)
(0.44+0.08j)
>>> print(x.conjugate())  # Сопряжённое число
(1-2j)
>>> print(x.imag)  # Мнимая часть
2.0
>>> print(x.real)  # Действительная часть
1.0
>>> print(x > y)  # Комплексные числа нельзя сравнить
Traceback (most recent call last):
  File "", line 1, in
TypeError: unorderable types: complex() > complex()
>>> print(x == y)  # Но можно проверить на равенство
False
>>> abs(3 + 4j)  # Модуль комплексного числа
5.0
>>> pow(3 + 4j, 2)  # Возведение в степень
(-7+24j)

Для работы с комплексными числами используется также модуль cmath.

Вещественные числа (float)

>>> 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1
0.9999999999999999

Для высокой точности используют другие объекты (например Decimal и Fraction)).

Также вещественные числа не поддерживают длинную арифметику:

>>> a = 3 ** 1000
>>> a + 0.1
Traceback (most recent call last):
  File "", line 1, in
OverflowError: int too large to convert to float

Простенькие примеры работы с числами:

>>> c = 150
>>> d = 12.9
>>> c + d
162.9
>>> p = abs(d - c)  # Модуль числа
>>> print(p)
137.1
>>> round(p)  # Округление
137

Умножение и деление

Операции умножения и деления, как сложение и вычитание, выполняются в Python так же, как в обычной математике. Для умножения Python использует *, для деления – /.

Например:

При делении в Python 3 частное всегда возвращается в виде числа с плавающей точкой, даже если вы делите целые числа:

Это одно из главных различий между Python 2 и Python 3. Python 3 возвращает дробный результат, потому при делении 11 на 2 вы получите 5.5. В Python 2 деление привязано к типам данных, потому при делении целого числа невозможно получить число с плавающей точкой; поэтому при делении 11 на 2 Python 2 возвращает 5.

Когда числа по обе стороны символа деления являются целыми, выполняется деление floor, то есть, для фактора х Python 2 возвращает наибольшее целое число меньше или равное х. К примеру, при делении 5 / 2 таким числом будет 2.

Чтобы выполнить деление floor и получить только целую часть числа, Python 3 использует оператор //. К примеру, разделив 100//40, вы получите 2.

Операции со строками

Строки в Python неизменяемые, вы не можете изменить один из символов строки. Любое изменение содержимого требует создания новой копии. Откройте интерпретатор и выполняйте перечисленные ниже примеры, для того чтобы лучше усвоить все написанное:

3. Объединение с преобразованием

Вы можете объединить строку с числом или логическим значением. Но для этого нужно использовать преобразование. Для этого существует функция str():

4. Поиск подстроки

Вы можете найти символ или подстроку с помощью метода find:

Этот метод выводит позицию первого вхождения подстроки losst.ru если она будет найдена, если ничего не найдено, то возвращается значение -1. Функция начинает поиск с первого символа, но вы можете начать с энного, например, 26:

В этом варианте функция вернет -1, поскольку строка не была найдена.

5. Получение подстроки

Мы получили позицию подстроки, которую ищем, а теперь как получить саму подстроку и то, что после нее? Для этого используйте такой синтаксис , просто укажите два числа или только первое:

Первая строка выведет подстроку от первого до второго символа, вторая — от второго и до конца

Обратите внимание, что отсчет начинается с нуля. Чтобы выполнять отсчет в обратном порядке, используйте отрицательное число

Вы можете заменить часть строки с помощью метода replace:

Если вхождений много, то можно заменить только первое:

7. Очистка строк

Вы можете удалить лишние пробелы с помощью функции strip:

Также можно удалить лишние пробелы только справа rstrip или только слева — lstrip.

Для изменения регистра символов существуют специальные функции:

9. Конвертирование строк

Есть несколько функций для конвертирования строки в различные числовые типы, это int(), float() , long() и другие. Функция int() преобразует в целое, а float() в число с плавающей точкой:

10. Длина строк

Вы можете использовать функции min(), max(), len() для расчета количества символов в строке:

Первая показывает минимальный размер символа, вторая — максимальный, а третья — общую длину строки.

11. Перебор строки

Вы можете получить доступ к каждому символу строки отдельно с помощью цикла for:

Для ограничения цикла мы использовали функцию len()

Обратите внимание на отступ. Программирование на python основывается на этом, здесь нет скобок для организации блоков, только отступы

Кавычки

Одинарные кавычки

Строку можно указать, используя одинарные кавычки, как например, ‘Это строка’. Любой одиночный символ в кавычках, например, ‘ю’ — это строка. Пустая строка » — это тоже строка. То есть строкой мы считаем всё, что находится внутри кавычек.

Двойные кавычки

Запись строки в одинарных кавычках это не единственный способ. Можно использовать и двойные кавычки, как например, »Это строка». Для интерпретатора разницы между записями строки в одинарных и двойных кавычках нет.

ВниманиеЕсли строка началась с двойной кавычки — значит и закончиться должна на двойной кавычке. Если внутри строки мы хотим использовать двойные кавычки, то саму строку надо делать в одинарных кавычках.

Театр »Современник»print(‘Театр »Современник»’)

Тройные кавычки

Строка, занимающая несколько строк, должна быть обрамлена тройными кавычками (» » » или »’). Например:

Целые числа и числа с плавающей запятой

Python имеет три встроенных числовых типа данных: целые числа, числа с плавающей запятой и комплексные числа. В этом разделе вы узнаете о целых числах и числах с плавающей запятой, которые являются двумя наиболее часто используемыми типами чисел. Вы узнаете о комплексных числах в следующем разделе.

Целые числа

Целое число – это целое число без десятичных знаков. Например, 1 – целое число, а 1.0 – нет. Имя для целочисленного типа данных – , которое вы можете увидеть с помощью :

Вы можете создать целое число, набрав желаемое число. Например, следующее присваивает переменной целое число 25:

Когда вы создаете такое целое число, значение 25 называется целочисленным литералом, потому что целое число буквально вводится в код.

Возможно, вы уже знакомы с тем, как преобразовать строку, содержащую целое число, в число с помощью . Например, следующее преобразует строку «25» в целое число 25:

не является целочисленным литералом, потому что целое значение создается из строки.

Когда вы пишете большие числа от руки, вы обычно группируете цифры в группы по три, разделенные запятой или десятичной точкой. Число 1000000 читать намного легче, чем число 1000000.

В Python нельзя использовать запятые для группировки цифр в целочисленных литералах, но можно использовать символы подчеркивания (_). Оба следующих способа являются допустимыми способами представления числа один миллион как целочисленного литерала:

Нет предела тому, насколько большим может быть целое число, что может быть удивительно, учитывая, что компьютеры имеют конечный объем памяти. Попробуйте ввести наибольшее число, которое вы можете придумать, в интерактивном окне IDLE. Python справится с этим без проблем!

Числа с плавающей запятой

Число с плавающей запятой(floating-point number) или сокращенно с плавающей запятой(float) – это число с десятичной запятой. 1.0 – это число с плавающей запятой, как и -2.75. Имя типа данных с плавающей запятой – float:

Как и целые числа, числа с плавающей запятой можно создавать из литералов с плавающей запятой(floating-point literals) или путем преобразования строки в число с плавающей запятой с помощью функции :

Есть три способа представить литерал с плавающей запятой. Каждое из следующих действий создает литерал с плавающей запятой со значением один миллион:

Первые два способа аналогичны двум методам создания целочисленных литералов. Третий подход использует нотацию E для создания литерала с плавающей запятой.

Чтобы написать литерал с плавающей запятой в нотации E, введите число, за которым следует буква e, а затем другое число. Python берет число слева от e и умножает его на 10, возведенное в степень числа после e. Итак, эквивалентно 1 × 10⁶.

Python также использует нотацию E для отображения больших чисел с плавающей запятой:

Число с плавающей запятой 200000000000000000.0 отображается как . Знак указывает, что показатель степени является положительным числом. Вы также можете использовать отрицательные числа в качестве показателя степени:

Литерал интерпретируется как в степени , что составляет 1/10000 или 0,0001.

В отличие от целых чисел, числа с плавающей запятой имеют максимальный размер. Максимальное число с плавающей запятой зависит от вашей системы, но что-то вроде должно выходить за рамки возможностей большинства машин. составляет 2 × 10⁴⁰⁰, что намного больше, чем общее количество атомов во Вселенной!

Когда вы достигнете максимального числа с плавающей запятой, Python вернет специальное значение с плавающей запятой, :

означает бесконечность, и это просто означает, что число, которое вы пытались создать, превышает максимальное значение с плавающей запятой, разрешенное на вашем компьютере. Тип по-прежнему :

Python также использует , что означает отрицательную бесконечность и представляет собой отрицательное число с плавающей запятой, которое превышает минимальное число с плавающей запятой, разрешенное на вашем компьютере:

Вы, вероятно, не будете часто сталкиваться с и как программист, если только вы не будете регулярно работать с очень большими числами.

7.5. Дискретное преобразование Фурье

Если данные в ваших массивах — это сигналы: звуки, изображения, радиоволны, котировки акций и т.д., то вам наверняка понадобится дискретное преобразование Фурье. В NumPy представлены методы быстрого дискретного преобразования Фурье для одномерных, двумерных и многомерных сигналов, а так же некоторые вспомогательные функции. Рассмотрим некоторые простые примеры.

Одномерное дискретное преобразование Фурье:

Двумерное дискретное преобразование Фурье:

Очень часто при спектральном анализе используются оконные функции (оконное преобразование Фурье), некоторые из которых так же представлены в NumPy

Список

Список (list) представляет тип данных, который хранит набор или последовательность элементов. Для создания списка в квадратных скобках через запятую перечисляются все его элементы.

Создание пустого списка

numbers = []

Создание списка чисел:

numbers =  # имя списка numbers, он содержит 5 элементов

Создание списка слов:

words = # имя списка words, он содержит 4 элемента

Создание списка из элементов разного типа

listNum =  # имя списка listNum,    список     содержит целые числа и строки

Для управления элементами списки имеют целый ряд методов. Некоторые из них:

append(item): добавляет элемент item в конец списка

insert(index, item): добавляет элемент item в список по индексу index

remove(item): удаляет элемент item. Удаляется только первое вхождение элемента. Если элемент не найден, генерирует исключение ValueError

clear(): удаление всех элементов из списка

index(item): возвращает индекс элемента item. Если элемент не найден, генерирует исключение ValueError

pop(): удаляет и возвращает элемент по индексу index. Если индекс не передан, то просто удаляет последний элемент.

count(item): возвращает количество вхождений элемента item в список

sort(): сортирует элементы. По умолчанию сортирует по возрастанию. Но с помощью параметра key мы можем передать функцию сортировки.

reverse(): расставляет все элементы в списке в обратном порядке

Кроме того, Python предоставляет ряд встроенных функций для работы со списками:

len(list): возвращает длину списка

sorted(list, ): возвращает отсортированный список

min(list): возвращает наименьший элемент списка

Операторы присваивания

Наиболее распространённым оператором присваивания является знак равенства (=). Он присваивает переменной слева значение справа. К примеру, в выражении v = 23 переменной v было присвоено значение 23.

В программировании часто используются составные операторы присваивания, которые выполняют операцию со значением переменной, а затем присваивают этой переменной полученное новое значение. Составные операторы объединяют арифметический оператор с оператором =. Например:

Составной оператор += выполнил сложение, а затем присвоил переменной w, значение, полученное в результате сложения.

Составные операторы часто используются в циклах.

Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.

В Python есть составные операторы присваивания для каждой математической операции:

Операторы присваивания позволяют постепенно увеличить или уменьшить значение, а также автоматизировать некоторые вычисления.

История

Возведение в степень – частный случай умножения, поэтому данную операцию изначально не рассматривали, как самостоятельную. Но уже в работах Диофанта Александрийского степени отведено особое место. В частности «Отец Алгебры» применял понятия кубов и квадратов числа.

Эта операция была известна ещё в древнем Вавилоне, однако современный её вид устоялся лишь в XVII веке.

Как умножение позволяет сократить количество символов сложения:

Так и степень сокращает запись умножения:

6 – это основание;
2 – показатель степени (это число говорит о том, сколько раз число в основании должно быть умножено само на себя).

До воцарения числового показателя, были и другие варианты его записи. Математики раннего Возрождения использовали буквы. Например, Q обозначала квадрат, а C – куб. Различные формы записи возведения в степень не обошли и языки программирования.

Операторы присваивания

Составные операторы часто используются в циклах.

for x in range (0, 7): x *= 2 print(x) 0 2 4 6 8 10 12

Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.

В Python есть составные операторы присваивания для каждой математической операции:

Дополнение 1: Как вызывать магические методы

Магический метод	Когда он вызывается (пример)	Объяснение
		вызывается при создании экземпляра
		вызывается при создании экземпляра
	, , etc.	Вызывается для любого сравнения
		Унарный знак плюса
		Унарный знак минуса
		Побитовая инверсия
		Преобразование, когда объект используется как индекс
	,	Булевое значение объекта
		Пытаются получить несуществующий атрибут
		Присвоение любому атрибуту
		Удаление атрибута
		Получить любой атрибут
		Получение элемента через индекс
		Присвоение элементу через индекс
		Удаление элемента через индекс
		Итерация
	,	Проверка принадлежности с помощью
		«Вызов» экземпляра
		оператор менеджеров контекста
		оператор менеджеров контекста
		Сериализация
		Сериализация

История

Эта операция была известна ещё в древнем Вавилоне, однако современный её вид устоялся лишь в XVII веке.

Как умножение позволяет сократить количество символов сложения:

6 + 6 + 6 + 6 + 6 + 6 = 6 * 6

Так и степень сокращает запись умножения:

Как посчитать сумму введенных чисел?

В команде input() можно передавать подсказки.

w = int(input(«Введите первое число: «)) q = int(input(«Введите второе число: «)) summa=w+q print(summa)

Введите первое число: 6 Введите второе число: 7 13

Копирование материалов разрешается только с указанием автора (Михаил Русаков) и индексируемой прямой ссылкой на сайт (http://myrusakov.ru)!

Добавляйтесь ко мне в друзья : http://vk.com/myrusakov.Если Вы хотите дать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.

Если Вы не хотите пропустить новые материалы на сайте,то Вы можете подписаться на обновления: Подписаться на обновления

Если у Вас остались какие-либо вопросы, либо у Вас есть желание высказаться по поводу этой статьи, то Вы можете оставить свой комментарий внизу страницы.

Порекомендуйте эту статью друзьям:

Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):

Как посчитать сумму введенных чисел?

В команде input() можно передавать подсказки.

w = int(input(«Введите первое число: «)) q = int(input(«Введите второе число: «)) summa=w+q print(summa)

Введите первое число: 6 Введите второе число: 7 13

Порекомендуйте эту статью друзьям:

Если Вам понравился сайт, то разместите ссылку на него (у себя на сайте, на форуме, в контакте):

7.3. Статистика

Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.

Элементарные статистические функции:

Средние значения элементов массива и их отклонения:

Корреляционные коэфициенты и ковариационные матрицы величин:

Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.

Модуль random

Модуль random предоставляет функции для генерации случайных чисел, букв, случайного выбора элементов последовательности. Модуль собрал разные функции для
имитации случайных процессов: , , , , ,
и другие.

Задание 4.3 Камень, ножницы, бумага

Запрограммируйте игру с компьютером в «Камень, ножницы, бумага». Пример диалога:

Счет 0:0
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 1
Мой ход: 2
Вы выиграли!
Счет 0:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 3
Мой ход: 3
Ничья!
Счет 0:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 1
Мой ход: 3
Вы проиграли!
Счет 1:1
Ваш ход (0-выход, 1-камень, 2-ножницы, 3-бумага): 0
Игра окончена со счетом 1:1

Квадратный корень — что это?

Квадратным корнем, полученным из числа «A», называют число «B», которое при возведении во 2-ю степень даст в итоге то самое изначальное число «A».

Непосредственную операцию, позволяющую найти значение «B», называют извлечением корня из «A». Математики применяют для обозначения этой операции специальный знак (его еще называют знаком радикала):

Когда речь идет о корне в «Питоне», ситуация обстоит иначе, причем в обоих случаях. К примеру, само возведение числа в степень записывают посредством оператора «**«:

Ответ в консоли «Пайтона» будет равняться четырем.

Касаемо квадратного корня, то он в Python представлен функцией sqrt(). Однако она существует не сама по себе, а в рамках соответствующего математического модуля math. Таким образом, перед началом работы этот модуль надо будет импортировать, но это абсолютно не сложно сделать на практике:

Идем дальше. Наша функция sqrt() принимает лишь один параметр – значение, из которого нам надо извлечь √. Давайте напишем простенький код и задействуем float в качестве типа данных возвращаемого значения.

Вы можете попробовать работу этого кода у себя на компьютере или на любом онлайн-компиляторе. Вот, к примеру, компилятор для Python 3.

Результат может быть таким:

Или таким:

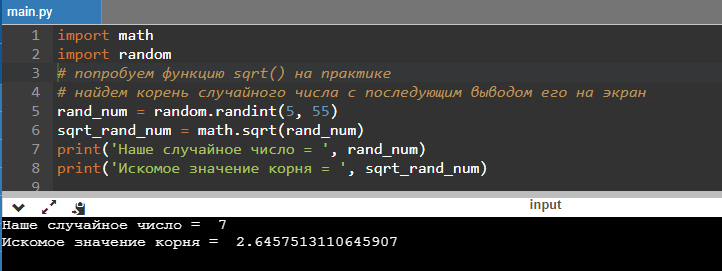
Так как мы используем модуль random, результат будет различаться при каждом выполнении кода.

Но никто не мешает сделать все намного проще:

Ответ очевиден:

Математические операторы Python 3

Ниже представлена таблица с кратким обзором математических операторов, доступных в Python.

Операция	Возвращаемое значение
x + y	Сумма x и y.
x — y	Разность x и y.
-x	Изменение знака x.
+x	Тождественность x.
x * y	Произведение x и y.
x / y	Частное от деления x на y.
x // y	Частное от целочисленного деления x на y.
x % y	Остаток от деления x / y.
x ** y	x в степени y.

Библиотека math

Для проведения вычислений с действительными числами язык Python содержит много дополнительных функций, собранных в библиотеку, которая называется math. Для использования этих функций в начале программы необходимо подключить библиотеку, что делается командой

import math # подключение модуля библиотеки

После подключения программа получает доступ ко всем функциям, методам и классам, содержащимся в нём. После подключения можно вызвать любую функцию из подключенной библиотеки по следующему правилу: указывается имя модуля и через точку имя функции

имя_модуля.имя_функции

Например, пусть мы хотим вызвать функцию вычисления Синус угла, задаваемого в радианахimport math y = sin(5) # ошибка не подключен модуль mathx = math.sin(5) # записываем имя модуля и через точку имя функции

Можно подключать не весь модуль, а какую-то его часть. Например, программист хочет использовать только одну функцию из математической библиотеки math. Если он подключит всю библиотеку, то будет добавлено более 40 функций, которые будут занимать место. Чтобы добавить в проект какую-то часть, используют ключевое слово from

from <имя подключаемого модуля> import <название функции>

Например.

from math import sin # подключена только одна функция siny = sin(5) # операция выполненаx = cos(5) # ошибка функция cos не подключена

Ниже приведен список основных функций модуля math. Некоторые из перечисленных функций (int, round, abs) являются стандартными и не требуют подключения модуля math для использования.