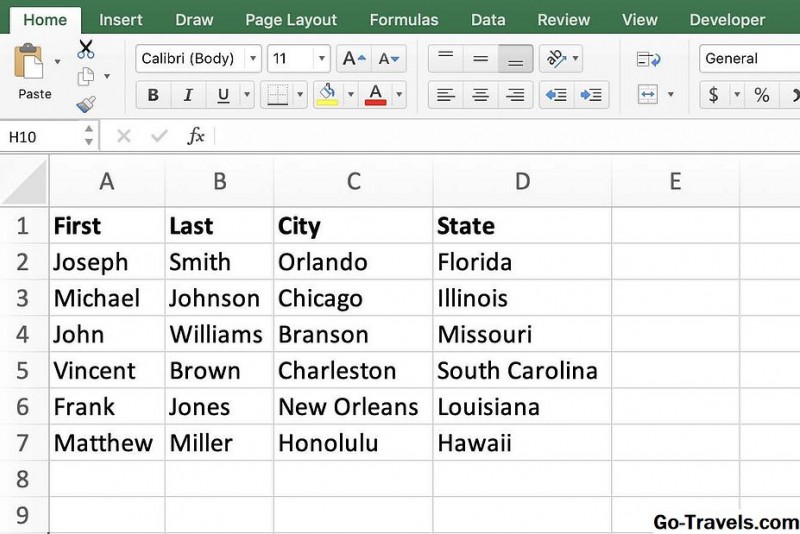
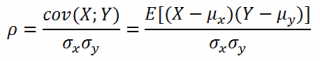Пример выполнения корреляционного анализа в excel
Содержание:
- Регрессия В Excel
- Пример регрессионного анализа №2
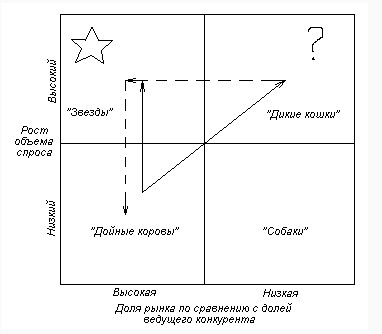
- Основные задачи и виды регрессии
- Разбор результатов анализа
- Коэффициент корреляции: что нужно знать, формула, пример расчёта в Excel
- Регрессионный анализ в Excel
- Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели
- Проверка общего качества уравнения множественной регрессии
- Пример регрессионного анализа №1
- Изучение результатов и выводы
Регрессия В Excel
Пакет анализаСервис/Надстройки
Excel 2007Параметры ExcelПараметры Excel

 НадстройкиПакет анализаПерейти
НадстройкиПакет анализаПерейти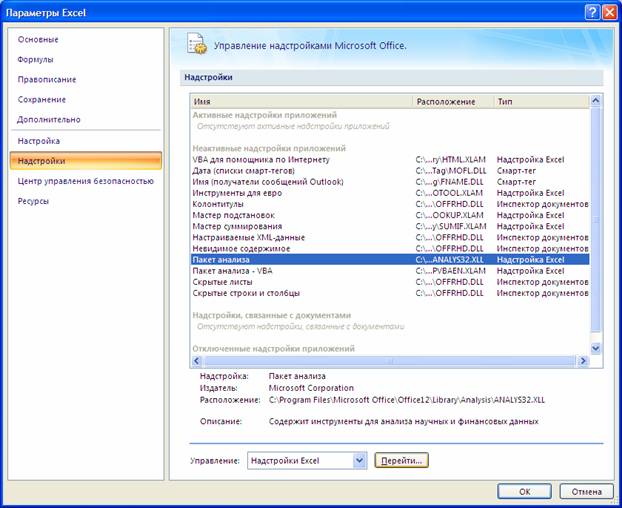
Для построения модели регрессии необходимо выбрать пункт . (В Excel 2007 этот режим находится в блоке ) Появится диалоговое окно, которое нужно заполнить:
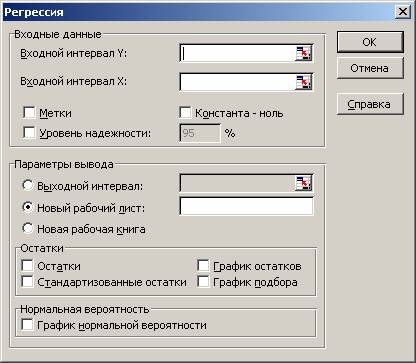 Входной интервалYyВходной интервалX12m(m≤16)МеткиУровень надежностиКонстанта-нольПараметры выводаНовый рабочий листОстатки
Входной интервалYyВходной интервалX12m(m≤16)МеткиУровень надежностиКонстанта-нольПараметры выводаНовый рабочий листОстатки
В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика, Дисперсионный анализ, Вывод остатка. Рассмотрим их подробнее.
1. Регрессионная статистика:
множественный R определяется формулой ;
R-квадрат вычисляется по формуле ;
Нормированный R-квадрат вычисляется по формуле ;
Стандартная ошибка S вычисляется по формуле ;
Наблюдения ¾ это количество данных n.
2. Дисперсионный анализ, строка Регрессия:
Параметр df равен m (количество наборов факторов x);
Параметр SS определяется формулой ;
Параметр MS определяется формулой ;
Статистика F определяется формулой ;
Значимость F. Если полученное число превышает α=1-p, то принимается гипотеза R2 = 0 (нет линейной зависимости), иначе принимается гипотеза R2≠0 (есть линейная зависимость).
3. Дисперсионный анализ, строка Остаток:
Параметр df равен n-m-1;
Параметр SS определяется формулой ;
Параметр MS определяется формулой .
4. Дисперсионный анализ, строка Итого содержит сумму первых двух столбцов.
5. Дисперсионный анализ, строка Y-пересечение содержит значение коэффициента a, стандартной ошибки Sb и t-статистики tb.
P-значение ¾ это значение уровней значимости, соответствующее вычисленным t-статистикам. Определяется функцией СТЬЮДРАСП(t-статистика; n—m-1). Если P-значение превышает α=1-p, то соответствующая переменная статистически незначима и ее можно исключить из модели.
Нижние 95% и Верхние 95% ¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.
6. Дисперсионный анализ, строки x1, x2,..,xm содержат значения коэффициентов, стандартных ошибок, t-статистик, P-значений и доверительных интервалов для соответствующих xi.
Блок Вывод остатка содержит значения предсказанного y (в наших обозначениях это ) и остатки .
Пример регрессионного анализа №2
Второй случай, в котором можно проводить регрессионный анализ – это необходимость найти максимальную модель распределения расходов на разные виды рекламы для того, чтобы получить самую большую прибыль. И такую маркетинговую задачу вполне может решить обычный Excel, кто бы мог подумать?
Предположим, максимальный бюджет на рекламу, который может быть потрачен организацией – 170000 рублей. Это ограничение невозможно предусмотреть стандартным средством, описанным выше. Здесь нужно использовать совсем другую надстройку, которая называется «Поиск решения». Есть ее возможность найти в том же разделе, что и описываемую нами. И аналогично пакету анализа, нам необходимо включить эту надстройку в том же самом меню.
Что же собой являет инструмент «Поиск решения»? Это надстройка, позволяющая найти оптимальный способ решения определенной задачи. Она имеет два основных параметра: целевая функция и ограничения. Таким образом, пользователь может находить оптимальную сумму затрат для рекламу в определенных условиях. Это одно из главных преимуществ данного инструмента.
Точно также, как в случае с пакетом анализа, инструмент поиска решения требует наличия математической модели. В качестве неё и выступает целевая функция. В нашем случае она следующая: Y= 2102438,6 + 6,4004 X1 – 54,068 X2 > max. В качестве используемых ограничений используется следующее выражение: X1 + X2 <= 170000, X1>= 0, X2 >=0.
После применения инструмента «Поиск решения» оказывается, что при заданных параметрах и ограничениях оптимально тратить деньги на рекламу по телевидению, поскольку это способно обеспечить максимальную прибыль. Как же пользоваться этим инструментом на практике? Для этого нужно выполнить следующие простые действия.
- Для начала нажать «Параметры Excel», после чего отправиться в категорию «Надстройки».
- После этого в поле «Управление» найти «Надстройки Excel» и кликнуть по «Перейти».
- После этого в списке надстроек активировать «Поиск решения».
После нажатия клавиши ОК надстройка успешно активирована. Далее достаточно просто нажимать на соответствующую кнопку на вкладке «Данные» в той же группе, что и пакет анализа и задать подходящие параметры. После этого программа все сделает самостоятельно. Таким образом, использование регрессии в Excel – очень простая штука. Значительно легче, чем может показаться на первый взгляд, поскольку большую часть действий выполняет программа. Достаточно просто вбить правильные настройки, и дальше можно расслабиться. И да, нужно еще интерпретировать результаты правильно. Но это не проблема. Успехов.
Основные задачи и виды регрессии
Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.
Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.
Основные задачи построения регрессионной модели заключаются в следующем:
- Отбор значимых независимых переменных (Х1, Х2, …, Xk).
- Выбор вида функции.
- Построение оценок для коэффициентов.
- Построение доверительных интервалов и функции регрессии.
- Проверка значимости вычисленных оценок и построенного уравнения регрессии.
Регрессионный анализ бывает нескольких видов:
- парный (1 зависимая и 1 независимая переменные);
- множественный (несколько независимых переменных).
Уравнения регрессии бывает двух видов:
- Линейные, иллюстрирующие строгую линейную связь между переменными.
- Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.
Инструкция построения модели
Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:
Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В MS EXCEL
1. Создайте файл исходных данных в MS Excel (например, таблица 2)
2. Построение корреляционного поля
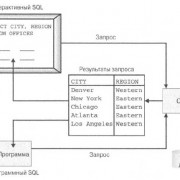
Для построения корреляционного поля в командной строке выбираем меню Вставка/ Диаграмма . В появившемся диалоговом окне выберите тип диаграммы: Точечная ; вид: Точечная диаграмма , позволяющая сравнить пары значений (Рис. 22).
Рисунок 22 – Выбор типа диаграммы
Рисунок 23– Вид окна при выборе диапазона и рядов Рисунок 25 – Вид окна, шаг 4
2. В контекстном меню выбираем команду Добавить линию тренда.
3. В появившемся диалоговом окне выбираем тип графика (в нашем примере линейная) и параметры уравнения, как показано на рисунке 26.
Нажимаем ОК. Результат представлен на рисунке 27.
Рисунок 27 – Корреляционное поле зависимости производительности труда от фондовооруженности
Аналогично строим корреляционное поле зависимости производительности труда от коэффициента сменности оборудования. (рисунок 28).
от коэффициента сменности оборудования
3. Построение корреляционной матрицы.
Для построения корреляционной матрицы в меню Сервис выбираем Анализ данных.
С помощью инструмента анализа данных Регрессия , помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Для этого необходимо проверить доступ к пакету анализа. В главном меню последовательно выберите Сервис/ Надстройки . Установите флажок Пакет анализа (Рисунок 29)
Рисунок 30 – Диалоговое окно Анализ данных
После нажатия ОК в появившемся диалоговом окне указываем входной интервал (в нашем примере А2:D26), группирование (в нашем случае по столбцам) и параметры вывода, как показано на рисунке 31.
Результат расчетов представлен в таблице 4.
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.

Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Мы рады, что смогли помочь Вам в решении проблемы.
Помогла ли вам эта статья?
Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
ŷ — ожидаемое значение у при заданном значении х,
x — независимая переменная,
a — отрезок на оси y для прямой линии,
b — наклон прямой линии.
На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением
На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4
Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.
Коэффициент корреляции: что нужно знать, формула, пример расчёта в Excel
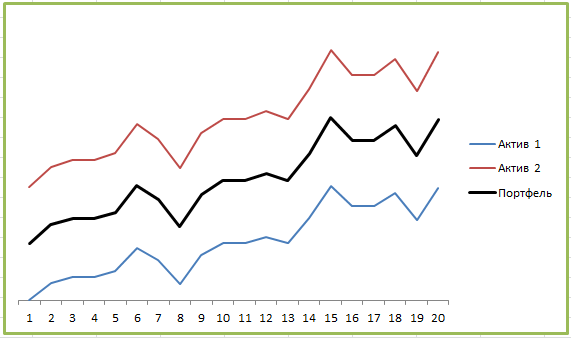
Приветствую всех читателей моего блога! Давненько я не писал статей по основам инвестирования. Сегодня хочу рассказать вам таком понятии как корреляция, которая имеет отношение к созданию качественного инвестиционного портфеля и диверсификации ваших вложений.
Если говорить о том, что такое корреляция простыми словами, то это по сути связь между двумя явлениями, выраженными в числовой форме. Например, проанализировав данные по ВВП на душу населения и продолжительности жизни в странах мира, мы невооруженным глазом заметим тенденцию:
А благодаря расчёту коэффициента корреляции мы можем узнать силу взаимосвязи в конкретном числовом выражении. Это очень удобно и полезно при анализе данных в самых разных областях науки, в том числе в экономике и инвестировании.
Сегодня я расскажу вам подробнее о том, что такое корреляция простыми словами, без сложных формул и терминов. Также я покажу вам, как правильно и легко рассчитать коэффициент корреляции в Excel и как правильно интерпретировать результаты, чтобы использовать их для составления инвестиционного портфеля.
А чтобы не пропускать следующие статьи блога, подписывайтесь на мой Телеграм-канал! Там же я выкладываю отчёты по инвестициям, сообщаю об обновлениях в моем инвест-портфеле и иногда пишу заметки на интересные темы. Даже чатик инвесторов у нас есть, присоединяйтесь
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации
В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Использование Пакета анализа EXCEL для построения множественной линейной регрессионной модели
Проведем множественный регрессионный анализ с помощью надстройки MS EXCEL Пакет анализа .
Эффективно использовать надстройку Пакет анализа могут только пользователи знакомые с теорией множественного регрессионного анализа .
В данной статье решены следующие задачи:
- Показано как в MS EXCEL выполнить регрессионный анализ с помощью надстройки Пакет анализа (инструмент Регрессия), т.е. как вызвать надстройку и правильно заполнить входные данные;
- Даны пояснения по разделам отчета, формированного надстройкой;
- Даны комментарии обо всех показателях, рассчитанных надстройкой, и приведены ссылки на соответствующие разделы статей, посвященные простой линейной регрессии .
В надстройке Пакет анализа для построения линейной регрессионной модели (как простой , так и множественной ) имеется специальный инструмент Регрессия .
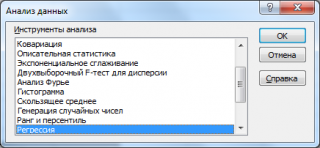
После выбора этого инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Надстройка ):
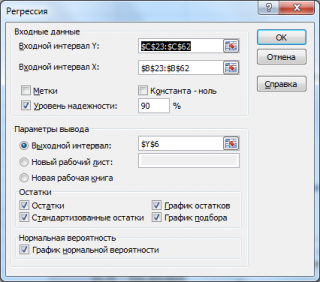
- Входной интервалY : ссылка на массив значений переменной Y. Ссылку можно указать с заголовком. В этом случае, при выводе результатов надстройка использует Ваш заголовок (для этого в окне требуется установить галочку Метки );
- Входной интервал Х : ссылка на значения переменных Х (нужно указать все столбцы со значениями Х). Ссылку рекомендуется делать на диапазон с заголовками (в окне не забудьте установить галочку Метки );
- Константа-ноль : если галочка установлена, то надстройка подбирает плоскость регрессии с b =0;
- Уровень надежности : Это значение используется для построения доверительных интервалов для наклона и сдвига . Уровень надежности = 1- альфа . Если галочка не установлена или установлена, но уровень значимости = 95%, то надстройка все равно рассчитывает границы доверительных интервалов, причем дублирует их. Если галочка установлена, а уровень надежности отличен от 95%, то рассчитываются 2 доверительных интервала : один для 95%, другой для введенного значения. Для демонстрации вышесказанного введем 90%;
- Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона;
- Остатки : будут вычислены остатки модели , т.е. разница между наблюденными и предсказанными значениями Yi для всех наблюдений n;
- Стандартизированные остатки : Вышеуказанные значения остатков будут поделены на значение их стандартного отклонения ;
- График остатков : Для каждой переменной X j будет построена точечная диаграмма : значения остатков и соответствующее значение Х ji (при прогнозировании на основании значений 2-х переменных Х будет построено 2 диаграммы (j=1 и 2));
- График подбора: Для каждой переменной X j будут построены точечные диаграммы с двумя рядами данных : точки данных (X ji ;Y i ) и (X ji ;Y iпредсказанное );
- График нормальной вероятности: Будет построена точечная диаграмма с названием График нормального распределения . По сути — это график значений переменной Y, отсортированных по возрастанию .
В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Надстройка , столбцы I:T).
Результаты вычислений, выполненных надстройкой, полностью совпадают с вычислениями сделанными нами в статье про множественную линейную регрессию с помощью функций ЛИНЕЙН() , ТЕНДЕНЦИЯ() и др. Использование альтернативных формул помогает разобраться с алгоритмом расчета показателей регрессии.
Отчет, сформированный надстройкой, состоит из следующих разделов:
Проверка общего качества уравнения множественной регрессии
Для этой цели, как и в случае множественной регрессии, используется коэффициентдетерминации R2:Справедливо соотношение 0 < =R2 < = 1. Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение Y.Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R2, так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведениезависимой переменной.Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится так называемый скорректированный (исправленный) коэффициент детерминации:Соотношение может быть представлено в следующем виде: для m>1. С ростом значения mскорректированный коэффициент детерминации растет медленнее, чем обычный.Очевидно, что только при R2 = 1. может принимать отрицательные значения. Доказано, что увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.Рекомендуется после проверки общего качества уравнения регрессии провести анализ его статистической значимости. Для этого используется F-статистика:
Показатели F и R2 равны или не равен нулю одновременно. Если F=0, то R2=0, следовательно, величина Y линейно не зависит от X1,X2,…,Xm.Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого уровня значимости α и чисел степеней свободы v1 = m и v2 = n — m — 1, определяется на основе распределения Фишера. Если F > Fкр, то R2 статистически значим.
Пример регрессионного анализа №1
А теперь настало время разобрать практические кейсы, как можно использовать линейную регрессию. Допустим, у нас есть набор данных о расходах на ТВ-рекламу, интернет-продвижение и о том, сколько получилось реализовать товара в российской национальной валюте. Все эти данные упакованы в таблицу. Перед нами стоит задача – определить коэффициенты регрессии для независимых переменных (то есть, в нашем случае ими выступают расходы на рекламу по ТВ и в интернете, поскольку оба значения влияют на объем реализуемых товаров). Последовательность действий такая:
- Открыть рабочий лист и ввести данные.
- Активировать инструмент регрессия способом, описанным выше.
- В появившемся диалоговом окне необходимо задать входной интервал X, Y, задать метки
- Также не стоит забывать ввести выходной интервал. Для выполнения этой задачи необходимо также указать такие параметры, как «График нормальной вероятности» и «График остатков».
Видим, что для этого кейса нам не нужно принципиально отходить от схемы, описанной выше. Линейная регрессия в этом случае позволяет уменьшить расходы на рекламу и увеличить отдачу от неё. То есть, выражаясь маркетинговым языком, увеличить ROMI – коэффициент возвратности инвестиций на маркетинг.
Изучение результатов и выводы
«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:
СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.
В более привычном математическом виде его можно записать, как:
y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844
Данные для АО «MMM» представлены в таблице:
Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.
Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.
Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.
Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.