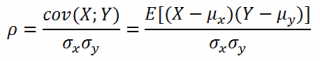Определитель матрицы

Как проводится корреляционный анализ в Excel

Суть данного анализа сводится к выявлению зависимостей между различными факторами, представленными в таблицах. Таким образом можно определить как повлияет уменьшение или увеличение определенных показателей на исследуемые данные.

Если была выявлена зависимость, то определяется уже коэффициент корреляции. Коэффициент будет варьироваться в значениях от -1 до +1. При положительной корреляции, увеличение одного показателя повлечет за собой увеличение другого. Соответственно при отрицательной будет уменьшение. Чем больше значение корреляции, тем сильнее оказываемое влияние.

Для примера возьмем таблицу, где представлена прямая зависимость одних показателей от других. Например, зарплата сотрудников и величина прибыли компании. Далее рассмотрим два способа реализации корреляционного анализа на примере этой таблицы.

Вариант 1: Вызов через Мастер функций

В отличии от некоторых других типов анализов, корреляционный анализ можно вызвать с помощью функций. За него отвечает функция КОРРЕЛ вида: КОРРЕЛ(массив1;массив2):

1. Выделите ячейку в таблицу, куда хотите вставить полученный результат. В строке ввода формул воспользуйтесь значком функции.

Откроется окно мастера функций. В поле “Категория” нужно поставить значение “Полный алфавитный перечень”, чтобы отобразились все доступные для применения функции. Там отыщите пункт “КОРРЕЛ” нажмите по нему и затем на кнопку “Ок”.</li>

Вам потребуется заполните в окошке настройки функции два поля, то есть указать два массива ячеек. В первый массив укажите номера ячеек, зависимость которых следует определить. Для рассматриваемой таблицы это будет массив столбца дохода компании. Номера можно вписать вручную или выделить их, кликнув по иконке таблицы в поле.</li>Во втором же массиве потребуется указать перечень ячеек, которые предположительно должны оказывать влияние на первый массив. В рассматриваемой таблице это величина зарплат сотрудников.</li>

Закончив с заполнением нажмите кнопку “Ок”. Подсчет будет произведен автоматически и выведен в указанной ранее ячейке.</li>Если полученный коэффициент оказался больше +/-0.5, то это значит, что одна величина сильно зависима от другой.</li></ol>

Вариант 2: Применение пакета анализа

Вы можете использовать уже заданный шаблон корреляционного анализа, используя один из представленных пакетов анализа. По умолчанию пакеты анализа в Excel отключены, поэтому вам потребуется их включать отдельно.

1. Перейдите во вкладку “Файл”, что расположена в верхней части окна.

В левой части переключитесь в раздел “Параметры”.</li>Откройте подраздел “Надстройки”, что находятся в левой части окна с параметрами.</li>У строки “Управление”, что расположена в нижней части открывшегося окна, установите значение “Надстройки Excel”. Нажмите “Перейти”, чтобы увидеть перечень доступных надстроек.</li>

В открывшемся окне установите галочку у пункта “Пакет анализа” и нажмите “Ок”. После этого у вас должны появится дополнительные инструменты в верхней панели Excel.</li>Нужные нам инструменты расположена во вклакде “Данные”. Там должен будет появится дополнительный блок инструментов — “Анализ”. Воспользуйтесь в нем единственным инструментом — “Анализом данных”.</li>

Открывается список с различными вариантами анализа данных. Укажите пункт “Корреляция”. Нажмите “Ок” для применения.</li>В открывшемся окошке настройки анализа уже потребуется заполнить только поле “Входной интервал”. Туда добавляется сразу два массива. В нашем случае это столбцы с зарплатой и доходом фирмы.</li>В блоке ниже можно указать, куда будет выводится результат. По умолчанию он выводит на новый рабочий лист, но вы можете настроить вывод в новую книгу или в определенных ячейках на текущем листе. Нажмите для применения и расчетов.</li>В итоге вы получите тот же результат, что и в первом способе. Единственное, в некоторых таблицах, при обработке большего количества данных значений может быть гораздо больше (в основном носят вспомогательный характер).</li></ol>

Первый рассмотренный нами способ подойдет для большинства таблиц, в то время как второй больше подходит для таблиц с большим перечнем данных, где еще желательно отследить логику проводимого анализа.

• https://lumpics.ru/correlation-analysis-in-excel/
• https://mir-tehnologiy.ru/korrelyatsiya-v-excel/
• https://exceltable.com/funkcii-excel/primery-funkcii-korrel
• https://public-pc.com/korrelyaczionnyj-analiz-v-excel/

Как рассчитать коэффициент корреляции

Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов. 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее. 

Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более. 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

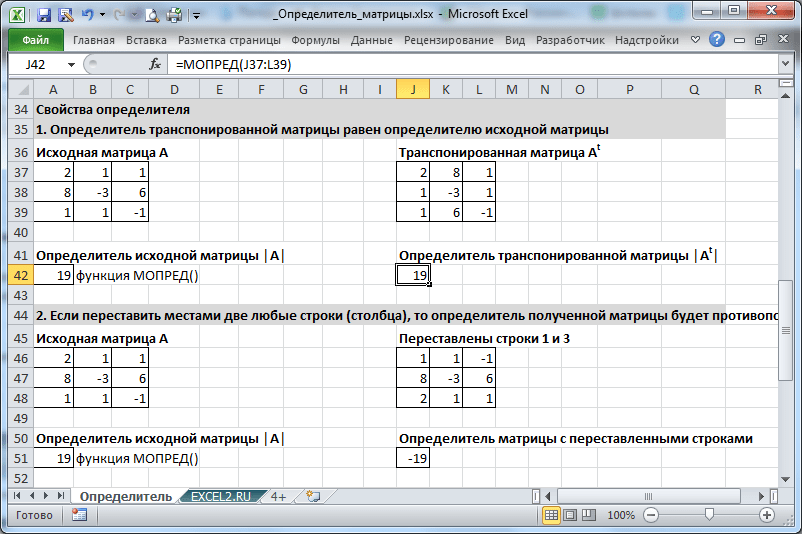
Свойства определителя

Теперь о некоторых свойствах определителя (см. файл примера
):

• Определитель равен определителю исходной матрицы
• Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
• Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
• Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на
  k
• Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
• det(А)=1/det(А -1), где А -1 — матрице А (А — квадратная невырожденная матрица).

пятница, 26 октября 2018 г.

Действия с матрицами в Excel

Для этого устанавливаем курсор мыши в ячейке В8 и удерживая левую кнопку мыши, растягиваем область выделения до ячейки Е14. Таким образом, мы выделили диапазон ячеек, куда должна вернуться транспонированная матрица. Далее, не снимая выделения, нажимаем на клавиатуре клавишу , а затем одновременно комбинацию кнопок + + . Чудо произошло! Весь выделенный диапазон заполнится нужными значениями!

Этот же прием мы будем неоднократно использовать ниже, во время умножения матриц друг на друга, а также нахождения обратной матрицы.

И, как обещал, еще один, очень быстрый способ транспонирования с помощью буфера обмена. Сначала выделяем диапазон ячеек В2:Н5 с исходной матрицей и во вкладке «Главная» нажимаем кнопку «Копировать». Затем устанавливаем курсор мыши в ячейку, начиная с которой мы хотим получить транспонированную матрицу. В нашем случае это ячейка В17.

Во вкладке «Главная» нажимаем кнопку «Вставить», «Специальная вставка». В открывшемся окне выделяем флаг «Транспонировать», как показано на рисунке, и нажимаем кнопку «ОК».

В результате диапазон ячеек В17:Е23 сразу же заполнится транспонированной матрицей!

Конечный результат матричных преобразований имеет вид:

2. Сложение матриц. Здесь нет никакой хитрости, все очень просто. Сложение выполняется для двух матриц одинаковой размерности. Каждый элемент суммарной матрицы равен сумме соответствующих элементов двух исходных матриц.

На данном рисунке в ячейках В2:D6 и F2:H6 приведены две исходные матрицы размерности 5х3, которые необходимо сложить.

В ячейках J2:L6 находится результирующая суммарная матрица. Как мы ее получили? Прежде всего, вводим в ячейку J2 формулу =B2+F2 и нажимаем .

Затем выделяем ячейку J2 еще раз, наводим острие курсора мыши на ее правый нижний угол, чтобы он принял вид крестика, и удерживая левую кнопку мыши, растягиваем формулу до ячейки L6.

3. Умножение матриц. Как было сказано выше, мы можем умножать матрицу на число или перемножать матрицы между собой.

В случае умножения исходной матрицы на число, мы должны каждый ее элемент умножить на это число, как показано на рисунке:

Исходная матрица находится в ячейках D4:F8. Умножим ее на число, которое записано в ячейке В6, то есть, на 12.

Для этого в ячейку Н4 я ввел формулу =D4*$B$6 и растянул ее за правый нижний угол до ячейки J8.

Умножение двух матриц выполняется встроенной функцией Excel =МУМНОЖ()

Здесь нужно обратить внимание:. Учитывая все вышесказанное, получим:

Учитывая все вышесказанное, получим:

В ячейках В14:D18 и F15:I17 находятся исходные матрицы, которые нужно перемножить. Первая матрица имеет 3 столбца, а вторая — 3 строки. То есть, первое правило выполняется.

В результате мы должны получить матрицу размерностью: 5х4. То есть, она должна иметь 5 строк, так как первая матрица тоже имеет 5 строк и должна иметь 4 столбца, так как вторая матрица имеет 4 столбца.

В ячейку К14 я ввел формулу: =МУМНОЖ(В14:D18;F15:I17) и нажал . А дальше имеем точно такую же ситуацию, как и с функцией =ТРАНСП(). Выделяем ячейки K14:N18 начиная с ячейки К14, нажимаем F2, а затем комбинацию + + .

В результате ячейки K14:N18 будут содержать результат умножения исходных матриц друг на друга.

4. Обратная матрица. Нахождение обратной матрицы связано с использованием встроенной функции =МОБР() и также имеет ограничение:

В ячейках В2:F6 содержится исходная квадратная не вырожденная матрица. Обратную матрицу будем находить в ячейках В9:F13. Для этого вводим в ячейку В9 формулу =МОБР(В2:F6) и нажимаем . Затем выделяем ячейки В9:F13 начиная с ячейки В9, нажимаем F2, а затем комбинацию + + . На этом все.

5. Определитель матрицы. Определитель матрицы будем находить с помощью встроенной функции =МОПРЕД(). Как и в случае с обратной матрицей, определитель мы будем находить только для квадратной матрицы.

По аналогии с предыдущим примером, пусть в ячейках В2:F6 содержится исходная квадратная не вырожденная матрица. Тогда, для нахождения ее определителя введем в ячейку В9 формулу =МОПРЕД(В2:F6).

В данном случае функция возвращает единственное число, а не массив значений, поэтому никаких дополнительных действий не требуется.

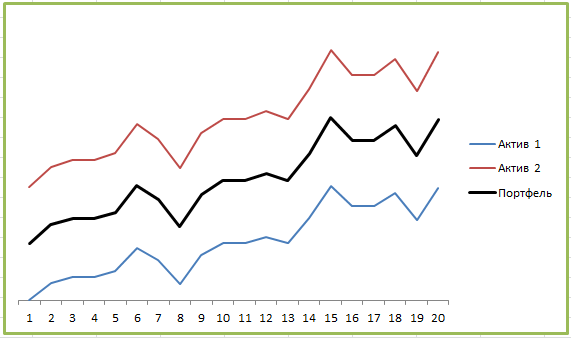
Строим диаграмму рассеяния (корреляционное поле) и график линии регрессии.

4.1.
Находим минимальный и максимальный элемент выборки X это 18-й и 15-й элементы соответственно, x min = 22.10000 и x max = 26.60000.

4.2.
Находим минимальный и максимальный элемент выборки Y это 2-й и 18-й элементы соответственно, y min = 29.40000 и y max = 31.60000.

4.3.
На оси абсцисс выбираем начальную точку чуть левее точки x 18
= 22.10000, и такой масштаб, чтобы на оси
поместилась точка x 15
= 26.60000 и отчетливо различались остальные точки.

4.4.
На оси ординат выбираем начальную точку чуть левее точки y 2
= 29.40000, и такой масштаб, чтобы на оси
поместилась точка y 18
= 31.60000 и отчетливо различались остальные точки.

4.5.
На оси абсцисс размещаем значения x k
, а на оси ординат значения y k
.

4.6.
Наносим точки (x 1
, y 1
),
(x 2
, y 2
),…,(x 26
, y 26
)
на координатную плоскость. Получаем диаграмму рассеяния (корреляционное поле), изображенное на рисунке ниже.

4.7.
Начертим линию регрессии.

Для этого найдем две различные точки с координатами (x r1 , y r1) и (x r2 , y r2)
удовлетворяющие уравнению (3.6), нанесем их на координатную плоскость и проведем через них прямую. В качестве абсциссы первой точки возьмем значение x min = 22.10000. Подставим значение x min в уравнение (3.6),
получим ординату первой точки. Таким образом имеем точку с координатами (22.10000, 31.96127). Аналогичным образом получим координаты второй точки, положив в качестве абсциссы значение x max = 26.60000.
Вторая точка будет: (26.60000, 30.15970).

Линия регрессии показана на рисунке ниже красным цветом

Обратите внимание, что линия регрессии всегда проходит через точку средних значений величин Х и Y, т.е. с координатами (M x , M y)

Утилита, которая широко используется во многих компаниях и на предприятиях. Реалии таковы, что практически любой работник должен в той или иной мере владеть Экселем, так как эта программа применяется для решения очень широкого спектра задач. Работая с таблицами, нередко приходится определять, связаны ли между собой определённые переменные. Для этого используется так называемая корреляция. В этой статье мы подробно рассмотрим, как рассчитать коэффициент корреляции в Excel. Давайте разбираться. Поехали!

Начнём с того, что такое коэффициент корреляции вообще. Он показывает степень взаимосвязи между двумя элементами и всегда находится в диапазоне от -1 (сильная обратная взаимосвязь) до 1 (сильная прямая взаимосвязь). Если коэффициент равен 0, это говорит о том, что взаимосвязь между значениями отсутствует.

Теперь, разобравшись с теорией, перейдём к практике. Чтобы найти взаимосвязь между переменными и у, воспользуйтесь встроенной функцией Microsoft Excel «КОРРЕЛ». Для этого нажмите на кнопку мастера функций (она расположена рядом с полем для формул). В открывшемся окне выберите из списка функций «КОРРЕЛ». После этого задайте диапазон в полях «Массив1» и «Массив2». Например, для «Массив1» выделите значения у, а для «Массив2» выделите значения х. В итоге вы получите рассчитанный программой коэффициент корреляции.

Следующий способ будет актуален для студентов, от которых требуют найти зависимость по заданной формуле. Прежде всего, нужно знать средние значения переменных x и y. Для этого выделите значения переменной и воспользуйтесь функцией «СРЗНАЧ». Далее необходимо вычислить разницу между каждым x и x ср, и y ср. В выбранных ячейках напишите формулы x-x, y-. Не забудьте закрепить ячейки со средними значениями. Затем растяните формулу вниз, чтобы она применилась и к остальным числам.

Теперь, когда есть все необходимые данные, можно посчитать корреляцию. Перемножьте полученные разности таким образом: (x-x ср) * (y-y ср). После того как вы получите результат для каждой из переменных, просуммируйте полученные числа при помощи функции автосуммы. Таким образом рассчитывается числитель.

Теперь перейдём к знаменателю. Посчитанные разности нужно возвести в квадрат. Для этого в отдельной колонке введите формулы: (x-x ср) 2 и (y-y ср) 2 . Затем растяните формулы на весь диапазон. После, при помощи кнопки «Автосумма», найдите сумму по всем колонкам (для x и для y). Осталось перемножить найденные суммы и извлечь из них квадратный корень. Последний шаг — поделите числитель на знаменатель. Полученный результат и будет искомым коэффициентом корреляции.

Как составить корреляционную матрицу в excel

Коэффициент линейной корреляции Браве-Пирсона ( ) — параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Он изменяется от (-1) (полная обратная линейная зависимость) до 1 (полная прямая пропорциональная зависимость). Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения случайных величин X и У.

В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ. Параметрами функции являются КОРРЕЛ (массив 1, массив 2), где:

• массив 1 — это диапазон ячеек первой случайной величины;

• массив 2 — это второй интервал ячеек со значениями второй случайной величины.

При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять из нескольких рядов числовых данных, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.

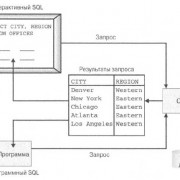
Корреляционная матрица — это квадратная (или прямоугольная) таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.

В MS Excel для вычисления корреляционных матриц используется процедура Корреляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо:

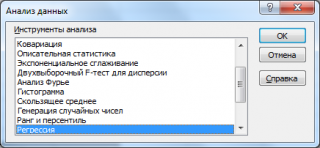
•выполнить команду Сервис ►Анализ данных;

•в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку 0К;

•в появившемся диалоговом окне указать Входной интервал, то есть ввести ссыл­ку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши. Входной интервал должен содержать не менее двух столбцов.

•в разделе Группировка переключатель установить в соответствии с введенными данными;

•указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.

Результаты анализа. В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.

Интерпретация результатов. Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Его числовое значение оценивается по эмпирическим правилам, изложенным в соответствующей лекции.

Ниже показаны две возможности вычисления коэффициента линейной корреляции Браве-Пирсона: на основе привлечения возможностей Мастера функций и на основе использования Пакета анализа.

Приведен пример исходных данных измерения двух показателей интеллекта (вербального (Х i ) и невербального (У i )) у 20 учащихся 8 класса. Рассчитать коэффициент корреляции.

Вербальный (Х i ): 13, 9, 8, 9, 7, 9, 8, 13, 11, 12, 8, 9, 10, 10, 12, 10, 8, 9, 10, 11.

Невербальный ( Yi ): 12, 11, 8, 12, 9, 11, 9, 13, 9, 10, 9, 8, 10, 12, 10, 10, 11, 10, 11, 13.

Результаты анализа. В результате будет получена таблица, показанная на рисунке.

Деление в экселе: как применяется, формула, примеры

Microsoft Office Excel имеет в своем наборе огромную библиотеку функций, которые позволяют проводить анализ числовых данных. Однако программа с легкостью может выступать в роли обычного калькулятора. Для этого в формулы с клавиатуры вставляются базовые математические операции и проводятся вычисления. Сегодня подробнее рассмотрим, как проводить деление в экселе.

Формула и примеры, как делить

Чтобы редактор проводил расчеты, необходимо для начала в активной ячейке поставить знак равно, после этого записать выражение. Сейчас разберем, как сделать деление, и рассмотрим основные варианты использования формулы.

Простые числа

В ячейке после знака равно ставите нужные цифры через знак деления, который на клавиатуре обозначается наклонной чертой. Его можно найти в цифровом блоке или справа от буквы ю на английской раскладке. То есть, чтобы в экселе поставить деление в формулу, достаточно нажать одну кнопку на клавиатуре.

На заметку! Можно одновременно использовать несколько операторов. Последовательность вычислений определена математическими законами: сначала умножение и деление, а потом сложение и вычитание.

Формула будет иметь следующий вид:

Ссылки на ячейки

Аналогичным образом можно использовать адреса ячеек внутри выражения. Тогда нужно четко указывать числитель и знаменатель.

Можно совмещать два предыдущих способа, если, например, знаменатель является неизменным численным значением.

Деление колонки на колонку

Достаточно часто нужно поделить один массив данных на другой. Для этого записываете выражение для одной строки и используете маркер автозаполнения, чтобы формула применялась для всего массива. Например, известна выручка от продажи партии продуктов, а также цена за единицу, необходимо найти количество проданных фруктов.

Решение задачи будет выглядеть следующим образом:

Аналогичным способом выполняется поиск решения, если числитель или знаменатель являются константой. Для этого необходимо зафиксировать значение внутри формулы, то есть сделать абсолютную ссылку на ячейку. Это можно сделать при помощи значка доллара или горячей клавиши F4.

Как известно из математики, провести деление на ноль нельзя. В редакторе также невозможно провести такую операцию. При этом достаточно не только нуля в знаменателе, но и пустой ячейки. Программа выдаст ошибку #ДЕЛ/0.

Функция

Помимо использования пользовательской формулы, в excel есть специальная функция, которая выводит результат в виде целых чисел. Она называется ЧАСТНОЕ. Выражение имеет два известных оператора – числитель и знаменатель.

Однако у этой функции есть одна особенность: в процессе работы округление происходит не по правилам математики, то есть после пяти в большую сторону, а до ближайшего целого. Для сравнения проведем операцию деления простейшей формулой.

Этот момент стоит учитывать при использовании данной функции.

Как видите, делить числа в эксель не сложно. Достаточно знать расположение знака деления на клавиатуре и правильно задать формулу. Если же используете специальную функцию, то помните про округление цифр до ближайшего целого.